模糊逻辑 - 会员函数

---

---

我们已经知道，模糊逻辑不是模糊的逻辑，而是用来描述模糊性的逻辑。这种模糊性最显著的特征就是它的隶属函数。换句话说，我们可以说隶属函数代表了模糊逻辑中的真值程度。

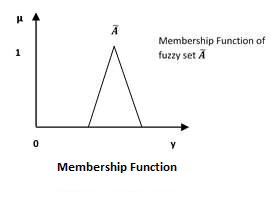
以下是一些与隶属函数相关的要点：

• 隶属函数最初由 Lotfi A. Zadeh 于 1965 年在其第一篇研究论文“模糊集”中提出。

• 隶属函数刻画了模糊性（即模糊集中所有信息），无论模糊集中的元素是离散的还是连续的。

• 隶属函数可以定义为一种通过经验而非知识来解决实际问题的技术。

• 隶属函数以图形形式表示。

• 定义模糊性的规则本身也是模糊的。

数学表示法

我们已经学习过，在信息宇宙 U 中的模糊集 Ã 可以定义为有序对的集合，可以用数学方式表示为：

$$\widetilde{A} = \left \{ \left ( y,\mu _{\widetilde{A}} \left ( y \right ) \right ) | y\in U\right \}$$

这里 $\mu \widetilde{A}\left (\bullet \right )$ = $\widetilde{A}$ 的隶属函数；它取值范围为 0 到 1，即 $\mu \widetilde{A}\left (\bullet \right )\in \left [ 0,1 \right ]$。隶属函数 $\mu \widetilde{A}\left (\bullet \right )$ 将 U 映射到隶属空间 M。

上述隶属函数中的点 $\left (\bullet \right )$ 代表模糊集中的元素；无论是离散的还是连续的。

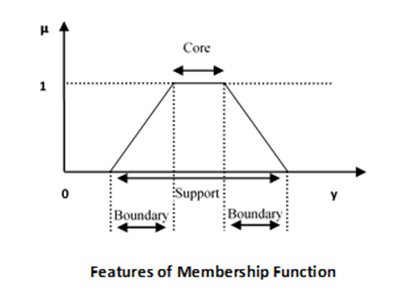
隶属函数的特征

现在我们将讨论隶属函数的不同特征。

核心

对于任何模糊集 $\widetilde{A}$，隶属函数的核心是宇宙中以完全隶属于该集合为特征的区域。因此，核心由信息宇宙中所有满足以下条件的元素 y 组成：

$$\mu _{\widetilde{A}}\left ( y \right ) = 1$$

支撑

对于任何模糊集 $\widetilde{A}$，隶属函数的支撑是宇宙中以非零隶属于该集合为特征的区域。因此，核心由信息宇宙中所有满足以下条件的元素 y 组成：

$$\mu _{\widetilde{A}}\left ( y \right ) > 0$$

边界

对于任何模糊集 $\widetilde{A}$，隶属函数的边界是宇宙中以非零但非完全隶属于该集合为特征的区域。因此，核心由信息宇宙中所有满足以下条件的元素 y 组成：

$$1 > \mu _{\widetilde{A}}\left ( y \right ) > 0$$

模糊化

可以定义为将清晰集转换为模糊集或将模糊集转换为更模糊集的过程。基本上，此操作将精确的清晰输入值转换为语言变量。

以下是两种重要的模糊化方法：

支撑模糊化（s-模糊化）方法

在这种方法中，模糊化后的集合可以用以下关系表示：

$$\widetilde{A} = \mu _1Q\left ( x_1 \right )+\mu _2Q\left ( x_2 \right )+...+\mu _nQ\left ( x_n \right )$$

这里模糊集 $Q\left ( x_i \right )$ 被称为模糊化的核。这种方法是通过保持 $\mu _i$ 常数并将其转换为模糊集 $Q\left ( x_i \right )$ 来实现的。

等级模糊化（g-模糊化）方法

它与上述方法非常相似，但主要区别在于它保持 $x_i$ 常数，并将 $\mu _i$ 表示为模糊集。

去模糊化

可以定义为将模糊集简化为清晰集或将模糊成员转换为清晰成员的过程。

我们已经学习过，模糊化过程涉及从清晰量到模糊量的转换。在许多工程应用中，需要对结果或更确切地说是“模糊结果”进行去模糊化，以便将其转换为清晰结果。从数学上讲，去模糊化过程也称为“四舍五入”。

下面描述了不同的去模糊化方法：

最大隶属度法

此方法仅限于峰值输出函数，也称为高度法。从数学上讲，它可以表示为：

$$\mu _{\widetilde{A}}\left ( x^* \right )>\mu _{\widetilde{A}}\left ( x \right ) \: for \:all\:x \in X$$

这里，$x^*$ 是去模糊化的输出。

质心法

此方法也称为面积中心法或重心法。从数学上讲，去模糊化的输出 $x^*$ 将表示为：

$$x^* = \frac{\int \mu _{\widetilde{A}}\left ( x \right ).xdx}{\int \mu _{\widetilde{A}}\left ( x \right ).dx}$$

加权平均法

在这种方法中，每个隶属函数都以其最大隶属度值加权。从数学上讲，去模糊化的输出 $x^*$ 将表示为：

$$x^* = \frac{\sum \mu _{\widetilde{A}}\left ( \overline{x_i} \right ).\overline{x_i}}{\sum \mu _{\widetilde{A}}\left ( \overline{x_i} \right )}$$

均值最大隶属度

此方法也称为最大值的中点。从数学上讲，去模糊化的输出 $x^*$ 将表示为：

$$x^* = \frac{\displaystyle \sum_{i=1}^{n}\overline{x_i}}{n}$$