模糊逻辑 - 集合论

---

---

模糊集可以被认为是经典集合的扩展和极度简化。它最好在集合成员关系的背景下理解。基本上，它允许部分成员关系，这意味着它包含在集合中具有不同程度成员关系的元素。由此，我们可以理解经典集合和模糊集之间的区别。经典集合包含满足精确成员属性的元素，而模糊集包含满足不精确成员属性的元素。

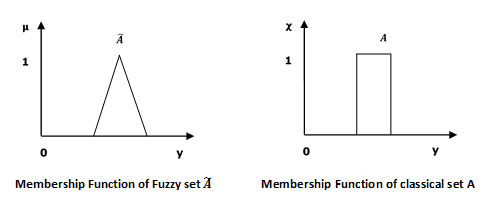
数学概念

信息宇宙 U 中的模糊集$\widetilde{A}$可以定义为一组有序对，可以用数学表示为：

$$\widetilde{A} = \left \{ \left ( y,\mu _{\widetilde{A}} \left ( y \right ) \right ) | y\in U\right \}$$

这里$\mu _{\widetilde{A}}\left ( y \right )$ = y 在 $\widetilde{A}$ 中的隶属度，取值范围为 0 到 1，即 $\mu _{\widetilde{A}}(y)\in \left [ 0,1 \right ]$。

模糊集的表示

现在让我们考虑信息宇宙的两种情况，并了解如何表示模糊集。

情况 1

当信息宇宙 U 是离散且有限时：

$$\widetilde{A} = \left \{ \frac{\mu _{\widetilde{A}}\left ( y_1 \right )}{y_1} +\frac{\mu _{\widetilde{A}}\left ( y_2 \right )}{y_2} +\frac{\mu _{\widetilde{A}}\left ( y_3 \right )}{y_3} +...\right \}$$

$= \left \{ \sum_{i=1}^{n}\frac{\mu _{\widetilde{A}}\left ( y_i \right )}{y_i} \right \}$

情况 2

当信息宇宙 U 是连续且无限时：

$$\widetilde{A} = \left \{ \int \frac{\mu _{\widetilde{A}}\left ( y \right )}{y} \right \}$$

在上述表示中，求和符号表示每个元素的集合。

模糊集的运算

对于两个模糊集 $\widetilde{A}$ 和 $\widetilde{B}$，信息宇宙 U 和宇宙中的一个元素 y，以下关系表示模糊集上的并集、交集和补集运算。

并集/模糊“或”

让我们考虑以下表示来理解并集/模糊“或”关系是如何工作的：

$$\mu _{{\widetilde{A}\cup \widetilde{B} }}\left ( y \right ) = \mu _{\widetilde{A}}\vee \mu _\widetilde{B} \quad \forall y \in U$$

这里 ∨ 表示“max”运算。

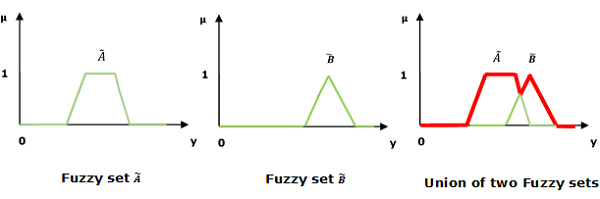
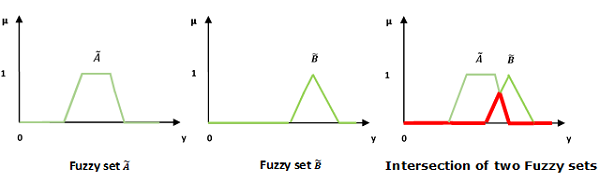
交集/模糊“与”

让我们考虑以下表示来理解交集/模糊“与”关系是如何工作的：

$$\mu _{{\widetilde{A}\cap \widetilde{B} }}\left ( y \right ) = \mu _{\widetilde{A}}\wedge \mu _\widetilde{B} \quad \forall y \in U$$

这里 ∧ 表示“min”运算。

补集/模糊“非”

让我们考虑以下表示来理解补集/模糊“非”关系是如何工作的：

$$\mu _{\widetilde{A}} = 1-\mu _{\widetilde{A}}\left ( y \right )\quad y \in U$$

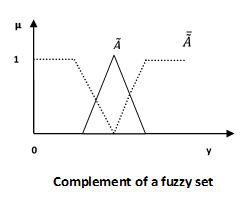
模糊集的性质

让我们讨论模糊集的不同性质。

交换律

对于两个模糊集 $\widetilde{A}$ 和 $\widetilde{B}$，此性质指出：

$$\widetilde{A}\cup \widetilde{B} = \widetilde{B}\cup \widetilde{A}$$

$$\widetilde{A}\cap \widetilde{B} = \widetilde{B}\cap \widetilde{A}$$

结合律

对于三个模糊集 $\widetilde{A}$，$\widetilde{B}$ 和 $\widetilde{C}$，此性质指出：

$$(\widetilde{A}\cup \left \widetilde{B}) \cup \widetilde{C} \right = \left \widetilde{A} \cup (\widetilde{B}\right )\cup \widetilde{C})$$

$$(\widetilde{A}\cap \left \widetilde{B}) \cap \widetilde{C} \right = \left \widetilde{A} \cup (\widetilde{B}\right \cap \widetilde{C})$$

分配律

对于三个模糊集 $\widetilde{A}$，$\widetilde{B}$ 和 $\widetilde{C}$，此性质指出：

$$\widetilde{A}\cup \left ( \widetilde{B} \cap \widetilde{C}\right ) = \left ( \widetilde{A} \cup \widetilde{B}\right )\cap \left ( \widetilde{A}\cup \widetilde{C} \right )$$

$$\widetilde{A}\cap \left ( \widetilde{B}\cup \widetilde{C} \right ) = \left ( \widetilde{A} \cap \widetilde{B} \right )\cup \left ( \widetilde{A}\cap \widetilde{C} \right )$$

幂等律

对于任何模糊集 $\widetilde{A}$，此性质指出：

$$\widetilde{A}\cup \widetilde{A} = \widetilde{A}$$

$$\widetilde{A}\cap \widetilde{A} = \widetilde{A}$$

恒等律

对于模糊集 $\widetilde{A}$ 和全集 U，此性质指出：

$$\widetilde{A}\cup \varphi = \widetilde{A}$$

$$\widetilde{A}\cap U = \widetilde{A}$$

$$\widetilde{A}\cap \varphi = \varphi$$

$$\widetilde{A}\cup U = U$$

传递律

对于三个模糊集 $\widetilde{A}$，$\widetilde{B}$ 和 $\widetilde{C}$，此性质指出：

$$如果 \: \widetilde{A}\subseteq \widetilde{B}\subseteq \widetilde{C},\:则\:\widetilde{A}\subseteq \widetilde{C}$$

对合律

对于任何模糊集 $\widetilde{A}$，此性质指出：

$$\overline{\overline{\widetilde{A}}} = \widetilde{A}$$

德摩根定律

该定律在证明重言式和矛盾方面起着至关重要的作用。该定律指出：

$$\overline{{\widetilde{A}\cap \widetilde{B}}} = \overline{\widetilde{A}}\cup \overline{\widetilde{B}}$$

$$\overline{{\widetilde{A}\cup \widetilde{B}}} = \overline{\widetilde{A}}\cap \overline{\widetilde{B}}$$