
- 模糊逻辑教程
- 模糊逻辑 - 首页
- 模糊逻辑 - 简介
- 模糊逻辑 - 经典集合论
- 模糊逻辑 - 集合论
- 模糊逻辑 -隶属函数
- 传统模糊逻辑复习
- 近似推理
- 模糊逻辑 - 推理系统
- 模糊逻辑 - 数据库和查询
- 模糊逻辑 - 量化
- 模糊逻辑 - 决策
- 模糊逻辑 - 控制系统
- 自适应模糊控制器
- 神经网络中的模糊性
- 模糊逻辑 - 应用
- 模糊逻辑有用资源
- 模糊逻辑 - 快速指南
- 模糊逻辑 - 有用资源
- 模糊逻辑 - 讨论
模糊逻辑 - 快速指南
模糊逻辑 - 简介
单词模糊指的是不明确或含糊的事物。任何持续变化的事件、过程或函数都不能总是被定义为真或假,这意味着我们需要以模糊的方式来定义此类活动。
什么是模糊逻辑?
模糊逻辑类似于人类的决策方法。它处理模糊和不精确的信息。这是对现实世界问题的极大简化,基于真值的程度,而不是像布尔逻辑那样的通常的真/假或1/0。
请看下图。它显示在模糊系统中,值由0到1范围内的数字表示。其中1.0表示绝对真,0.0表示绝对假。表示模糊系统中值的数字称为真值。
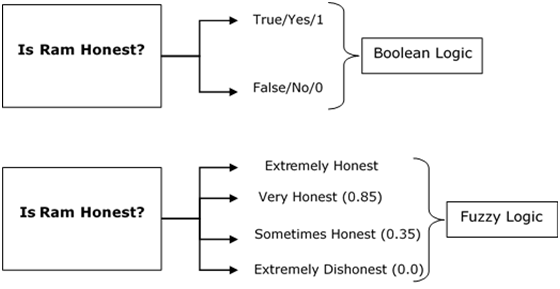
换句话说,我们可以说模糊逻辑不是模糊的逻辑,而是用于描述模糊性的逻辑。我们可以用许多其他例子来理解模糊逻辑的概念。
模糊逻辑由Lotfi A. Zadeh于1965年在他的研究论文“模糊集”中提出。他被认为是模糊逻辑之父。
模糊逻辑 - 经典集合论
集合是不同元素的无序集合。可以使用集合括号列出其元素来明确地写出它。如果元素的顺序改变或集合的任何元素重复,则不会对集合进行任何更改。
例子
- 所有正整数的集合。
- 太阳系中所有行星的集合。
- 印度所有邦的集合。
- 字母表中所有小写字母的集合。
集合的数学表示
集合可以用两种方式表示:
枚举法或表格法
在这种形式中,集合通过列出构成它的所有元素来表示。元素用大括号括起来,并用逗号分隔。
以下是枚举法或表格法中集合的例子:
- 英语字母表中的元音集合,A = {a,e,i,o,u}
- 小于10的奇数集合,B = {1,3,5,7,9}
集合构造法
在这种形式中,集合是通过指定集合元素共有的属性来定义的。集合被描述为A = {x:p(x)}
示例1 - 集合{a,e,i,o,u}写成
A = {x:x是英语字母表中的元音}
示例2 - 集合{1,3,5,7,9}写成
B = {x:1 ≤ x < 10 且 (x%2) ≠ 0}
如果元素x是任何集合S的成员,则表示为x∈S;如果元素y不是集合S的成员,则表示为y∉S。
示例 - 如果S = {1,1.2,1.7,2},则1 ∈ S,但1.5 ∉ S
集合的基数
集合S的基数,记为|S|,是集合的元素个数。这个数也称为基数。如果一个集合有无限多个元素,则它的基数是∞。
示例 - |{1,4,3,5}| = 4,|{1,2,3,4,5,…}| = ∞
如果有两个集合X和Y,|X| = |Y|表示两个集合X和Y具有相同的基数。当X中的元素个数正好等于Y中的元素个数时,就会发生这种情况。在这种情况下,存在从X到Y的双射函数'f'。
|X| ≤ |Y|表示集合X的基数小于或等于集合Y的基数。当X中的元素个数小于或等于Y中的元素个数时,就会发生这种情况。这里,存在从X到Y的单射函数'f'。
|X| < |Y|表示集合X的基数小于集合Y的基数。当X中的元素个数小于Y中的元素个数时,就会发生这种情况。这里,从X到Y的函数'f'是单射函数,但不是双射函数。
如果|X| ≤ |Y|并且|X| ≥ |Y|,则|X| = |Y|。集合X和Y通常称为等价集合。
集合的类型
集合可以分为许多类型;其中一些是有限集、无限集、子集、全集、真子集、单元素集等。
有限集
包含一定数量元素的集合称为有限集。
示例 - S = {x|x ∈ N 且 70 > x > 50}
无限集
包含无限多个元素的集合称为无限集。
示例 - S = {x|x ∈ N 且 x > 10}
子集
如果集合X的每个元素都是集合Y的元素,则集合X是集合Y的子集(写成X ⊆ Y)。
示例1 - 令X = {1,2,3,4,5,6}且Y = {1,2}。这里集合Y是集合X的子集,因为集合Y的所有元素都在集合X中。因此,我们可以写成Y⊆X。
示例2 - 令X = {1,2,3}且Y = {1,2,3}。这里集合Y是集合X的子集(而不是真子集),因为集合Y的所有元素都在集合X中。因此,我们可以写成Y⊆X。
真子集
术语“真子集”可以定义为“是子集,但不等于”。如果集合X的每个元素都是集合Y的元素,并且|X| < |Y|,则集合X是集合Y的真子集(写成X ⊂ Y)。
示例 - 令X = {1,2,3,4,5,6}且Y = {1,2}。这里集合Y ⊂ X,因为Y中的所有元素也包含在X中,并且X至少有一个比集合Y多的元素。
全集
它是特定上下文或应用程序中所有元素的集合。该上下文或应用程序中的所有集合本质上都是这个全集的子集。全集表示为U。
示例 - 我们可以将U定义为地球上所有动物的集合。在这种情况下,所有哺乳动物的集合是U的子集,所有鱼类的集合是U的子集,所有昆虫的集合是U的子集,等等。
空集或null集
空集不包含任何元素。它用Φ表示。由于空集中的元素数量是有限的,因此空集是有限集。空集或null集的基数为零。
示例 – S = {x|x ∈ N 且 7 < x < 8} = Φ
单元素集或单元集
单元素集或单元集只包含一个元素。单元素集表示为{s}。
示例 - S = {x|x ∈ N,7 < x < 9} = {8}
相等集合
如果两个集合包含相同的元素,则它们被称为相等。
示例 - 如果A = {1,2,6}且B = {6,1,2},则它们相等,因为集合A的每个元素都是集合B的元素,并且集合B的每个元素都是集合A的元素。
等价集合
如果两个集合的基数相同,则它们被称为等价集合。
示例 - 如果A = {1,2,6}且B = {16,17,22},则它们是等价的,因为A的基数等于B的基数。即|A| = |B| = 3
重叠集合
至少有一个公共元素的两个集合称为重叠集合。对于重叠集合:
$$n\left ( A\cup B \right ) = n\left ( A \right ) + n\left ( B \right ) - n\left ( A\cap B \right )$$
$$n\left ( A\cup B \right ) = n\left ( A-B \right )+n\left ( B-A \right )+n\left ( A\cap B \right )$$
$$n\left ( A \right ) = n\left ( A-B \right )+n\left ( A\cap B \right )$$
$$n\left ( B \right ) = n\left ( B-A \right )+n\left ( A\cap B \right )$$
示例 - 令A = {1,2,6}且B = {6,12,42}。有一个公共元素'6',因此这些集合是重叠集合。
不相交集合
如果两个集合A和B没有任何公共元素,则它们被称为不相交集合。因此,不相交集合具有以下性质:
$$n\left ( A\cap B \right ) = \phi$$
$$n\left ( A\cup B \right ) = n\left ( A \right )+n\left ( B \right )$$
示例 - 令A = {1,2,6}且B = {7,9,14},没有一个公共元素,因此这些集合是重叠集合。(此处应为不相交集合)
经典集合上的运算
集合运算包括集合并、集合交、集合差、集合补和笛卡尔积。
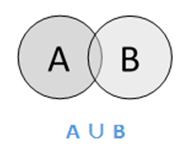
并集
集合A和B的并集(记作A ∪ B)是属于A、属于B或同时属于A和B的元素的集合。因此,A ∪ B = {x|x ∈ A 或 x ∈ B}。
示例 - 如果A = {10,11,12,13}且B = {13,14,15},则A ∪ B = {10,11,12,13,14,15} - 公共元素只出现一次。
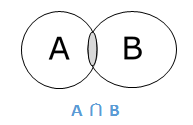
交集
集合A和B的交集(记作A ∩ B)是同时属于A和B的元素的集合。因此,A ∩ B = {x|x ∈ A 且 x ∈ B}。
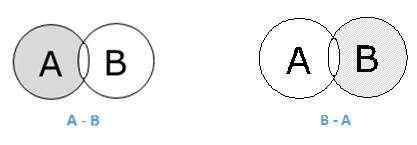
差集/相对补集
集合A和B的差集(记作A–B)是只属于A而不属于B的元素的集合。因此,A − B = {x|x ∈ A 且 x ∉ B}。
示例 - 如果A = {10,11,12,13}且B = {13,14,15},则(A − B) = {10,11,12}且(B − A) = {14,15}。在这里,我们可以看到(A − B) ≠ (B − A)
集合的补集
集合A的补集(记作A′)是不属于集合A的元素的集合。因此,A′ = {x|x ∉ A}。
更具体地说,A′ = (U−A),其中U是包含所有对象的全集。
示例 - 如果A = {x|x属于奇整数集合},则A′ = {y|y不属于奇整数集合}
笛卡尔积/交叉积
n个集合A1,A2,…An的笛卡尔积,记作A1 × A2...× An,可以定义为所有可能的序对(x1,x2,…xn),其中x1 ∈ A1,x2 ∈ A2,…xn ∈ An
示例 - 如果我们取两个集合A = {a,b}和B = {1,2},
A和B的笛卡尔积写成:A × B = {(a,1),(a,2),(b,1),(b,2)}
B与A的笛卡尔积写成− B × A = {(1,a),(1,b),(2,a),(2,b)}
经典集合的性质
集合的性质在获得解的过程中起着重要作用。以下是经典集合的不同性质:
交换律
对于两个集合A和B,该性质指出:
$$A \cup B = B \cup A$$
$$A \cap B = B \cap A$$
结合律
对于三个集合A、B和C,该性质指出:
$$A\cup \left ( B\cup C \right ) = \left ( A\cup B \right )\cup C$$
$$A\cap \left ( B\cap C \right ) = \left ( A\cap B \right )\cap C$$
分配律
对于三个集合A、B和C,该性质指出:
$$A\cup \left ( B\cap C \right ) = \left ( A\cup B \right )\cap \left ( A\cup C \right )$$
$$A\cap \left ( B\cup C \right ) = \left ( A\cap B \right )\cup \left ( A\cap C \right )$$
幂等律
对于任何集合A,该性质指出:
$$A\cup A = A$$
$$A\cap A = A$$
恒等律
对于集合A和全集X,该性质指出:
$$A\cup \varphi = A$$
$$A\cap X = A$$
$$A\cap \varphi = \varphi$$
$$A\cup X = X$$
传递律
对于三个集合A、B和C,该性质指出:
如果 $A\subseteq B\subseteq C$,则 $A\subseteq C$
对合律
对于任何集合A,该性质指出:
$$\overline{{\overline{A}}} = A$$
德摩根律
这是一个非常重要的定律,它有助于证明重言式和矛盾。该定律指出:
$$\overline{A\cap B} = \overline{A} \cup \overline{B}$$
$$\overline{A\cup B} = \overline{A} \cap \overline{B}$$
模糊逻辑 - 集合论
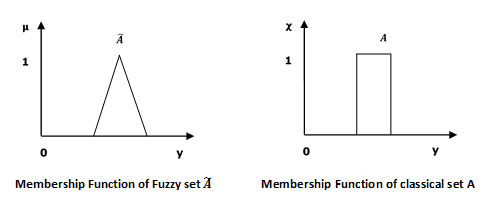
模糊集可以被认为是经典集合的扩展和粗略简化。它最好在集合成员资格的背景下理解。基本上,它允许部分成员资格,这意味着它包含具有不同成员资格程度的元素。由此,我们可以理解经典集合和模糊集之间的区别。经典集合包含满足精确成员资格属性的元素,而模糊集包含满足不精确成员资格属性的元素。
数学概念
信息宇宙U中的模糊集$\widetilde{A}$可以定义为一组有序对,可以用数学表示为:
$$\widetilde{A} = \left \{ \left ( y,\mu _{\widetilde{A}} \left ( y \right ) \right ) | y\in U\right \}$$
这里$\mu _{\widetilde{A}}\left ( y \right )$ = y在$\widetilde{A}$中的隶属度,取值范围为0到1,即$\mu _{\widetilde{A}}(y)\in \left [ 0,1 \right ]$。
模糊集的表示
现在让我们考虑信息宇宙的两种情况,并了解如何表示模糊集。
情况1
当信息宇宙U是离散且有限的:
$$\widetilde{A} = \left \{ \frac{\mu _{\widetilde{A}}\left ( y_1 \right )}{y_1} +\frac{\mu _{\widetilde{A}}\left ( y_2 \right )}{y_2} +\frac{\mu _{\widetilde{A}}\left ( y_3 \right )}{y_3} +...\right \}$$
$= \left \{ \sum_{i=1}^{n}\frac{\mu _{\widetilde{A}}\left ( y_i \right )}{y_i} \right \}$
情况2
当信息宇宙U是连续且无限的:
$$\widetilde{A} = \left \{ \int \frac{\mu _{\widetilde{A}}\left ( y \right )}{y} \right \}$$
在上述表示中,求和符号代表每个元素的集合。
模糊集上的运算
对于两个模糊集$\widetilde{A}$和$\widetilde{B}$,信息宇宙U和宇宙中的一个元素y,以下关系表示模糊集上的并、交和补运算。
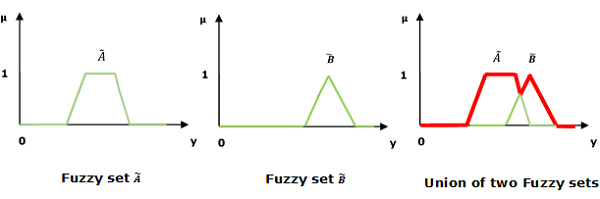
并/模糊“或”
让我们考虑以下表示来理解并/模糊“或”关系是如何工作的:
$$\mu _{{\widetilde{A}\cup \widetilde{B} }}\left ( y \right ) = \mu _{\widetilde{A}}\vee \mu _\widetilde{B} \quad \forall y \in U$$
这里∨代表“最大”运算。
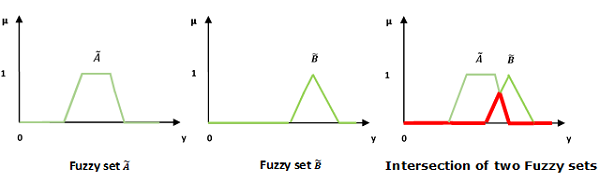
交/模糊“与”
让我们考虑以下表示来理解交/模糊“与”关系是如何工作的:
$$\mu _{{\widetilde{A}\cap \widetilde{B} }}\left ( y \right ) = \mu _{\widetilde{A}}\wedge \mu _\widetilde{B} \quad \forall y \in U$$
这里∧代表“最小”运算。
补/模糊“非”
让我们考虑以下表示来理解补/模糊“非”关系是如何工作的:
$$\mu _{\widetilde{A}} = 1-\mu _{\widetilde{A}}\left ( y \right )\quad y \in U$$
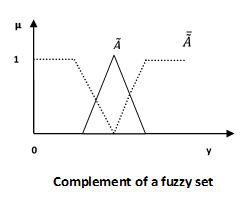
模糊集的性质
让我们讨论模糊集的不同性质。
交换律
对于两个模糊集$\widetilde{A}$和$\widetilde{B}$,该性质指出:
$$\widetilde{A}\cup \widetilde{B} = \widetilde{B}\cup \widetilde{A}$$
$$\widetilde{A}\cap \widetilde{B} = \widetilde{B}\cap \widetilde{A}$$
结合律
对于三个模糊集$\widetilde{A}$、$\widetilde{B}$和$\widetilde{C}$,该性质指出:
$$(\widetilde{A}\cup \widetilde{B}) \cup \widetilde{C} = \widetilde{A} \cup (\widetilde{B}\cup \widetilde{C})$$
$$(\widetilde{A}\cap \widetilde{B}) \cap \widetilde{C} = \widetilde{A} \cap (\widetilde{B}\cap \widetilde{C})$$
分配律
对于三个模糊集$\widetilde{A}$、$\widetilde{B}$和$\widetilde{C}$,该性质指出:
$$\widetilde{A}\cup \left ( \widetilde{B} \cap \widetilde{C}\right ) = \left ( \widetilde{A} \cup \widetilde{B}\right )\cap \left ( \widetilde{A}\cup \widetilde{C} \right )$$
$$\widetilde{A}\cap \left ( \widetilde{B}\cup \widetilde{C} \right ) = \left ( \widetilde{A} \cap \widetilde{B} \right )\cup \left ( \widetilde{A}\cap \widetilde{C} \right )$$
幂等律
对于任何模糊集$\widetilde{A}$,该性质指出:
$$\widetilde{A}\cup \widetilde{A} = \widetilde{A}$$
$$\widetilde{A}\cap \widetilde{A} = \widetilde{A}$$
恒等律
对于模糊集$\widetilde{A}$和全集U,该性质指出:
$$\widetilde{A}\cup \varphi = \widetilde{A}$$
$$\widetilde{A}\cap U = \widetilde{A}$$
$$\widetilde{A}\cap \varphi = \varphi$$
$$\widetilde{A}\cup U = U$$
传递律
对于三个模糊集$\widetilde{A}$、$\widetilde{B}$和$\widetilde{C}$,该性质指出:
$$如果 \: \widetilde{A}\subseteq \widetilde{B}\subseteq \widetilde{C},\:则\:\widetilde{A}\subseteq \widetilde{C}$$
对合律
对于任何模糊集$\widetilde{A}$,该性质指出:
$$\overline{\overline{\widetilde{A}}} = \widetilde{A}$$
德摩根律
该定律在证明重言式和矛盾中起着至关重要的作用。该定律指出:
$$\overline{{\widetilde{A}\cap \widetilde{B}}} = \overline{\widetilde{A}}\cup \overline{\widetilde{B}}$$
$$\overline{{\widetilde{A}\cup \widetilde{B}}} = \overline{\widetilde{A}}\cap \overline{\widetilde{B}}$$
模糊逻辑 -隶属函数
我们已经知道,模糊逻辑不是模糊的逻辑,而是用于描述模糊性的逻辑。这种模糊性最好用其隶属函数来表征。换句话说,我们可以说隶属函数表示模糊逻辑中的真值程度。
以下是关于隶属函数的一些要点:
隶属函数最早由Lotfi A. Zadeh于1965年在其第一篇研究论文“模糊集”中提出。
隶属函数表征模糊性(即模糊集中的所有信息),无论模糊集中的元素是离散的还是连续的。
隶属函数可以定义为通过经验而不是知识来解决实际问题的技术。
隶属函数以图形形式表示。
定义模糊性的规则也是模糊的。
数学符号
我们已经学习过,信息宇宙U中的模糊集$\widetilde{A}$可以定义为一组有序对,可以用数学表示为:
$$\widetilde{A} = \left \{ \left ( y,\mu _{\widetilde{A}} \left ( y \right ) \right ) | y\in U\right \}$$
这里$\mu_{\widetilde{A}}(\bullet)$ = $\widetilde{A}$的隶属函数;其取值范围为0到1,即$\mu_{\widetilde{A}}(\bullet) \in [0, 1]$。隶属函数$\mu_{\widetilde{A}}(\bullet)$ 将U映射到隶属空间M。
上述隶属函数中的点$(\bullet)$表示模糊集中的元素;无论是离散的还是连续的。
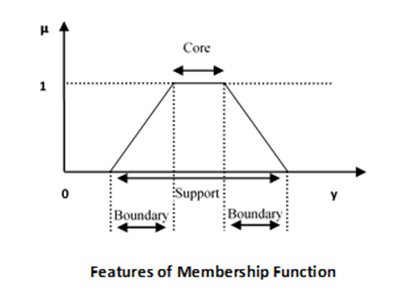
隶属函数的特征
我们现在将讨论隶属函数的不同特征。
核
对于任何模糊集$\widetilde{A}$,隶属函数的核是宇宙中以完全隶属于集合为特征的区域。因此,核由信息宇宙的所有那些元素y组成,使得:
$$\mu _{\widetilde{A}}\left ( y \right ) = 1$$
支集
对于任何模糊集$\widetilde{A}$,隶属函数的支集是宇宙中以非零隶属于集合为特征的区域。因此,核由信息宇宙的所有那些元素y组成,使得:
$$\mu _{\widetilde{A}}\left ( y \right ) > 0$$
边界
对于任何模糊集$\widetilde{A}$,隶属函数的边界是宇宙中以非零但非完全隶属于集合为特征的区域。因此,核由信息宇宙的所有那些元素y组成,使得:
$$1 > \mu _{\widetilde{A}}\left ( y \right ) > 0$$
模糊化
它可以定义为将清晰集转换为模糊集或将模糊集转换为更模糊集的过程。基本上,此操作将精确的清晰输入值转换为语言变量。
以下是两种重要的模糊化方法:
支集模糊化(s-模糊化)方法
在这种方法中,模糊集可以用以下关系表示:
$$\widetilde{A} = \mu _1Q\left ( x_1 \right )+\mu _2Q\left ( x_2 \right )+...+\mu _nQ\left ( x_n \right )$$
这里模糊集$Q\left ( x_i \right )$被称为模糊化的核。该方法通过保持$\mu _i$不变,并将$x_i$转换为模糊集$Q\left ( x_i \right )$来实现。
等级模糊化(g-模糊化)方法
它与上述方法非常相似,但主要区别在于它保持$x_i$不变,并将$\mu _i$表示为模糊集。
去模糊化
它可以定义为将模糊集简化为清晰集或将模糊成员转换为清晰成员的过程。
我们已经学习过,模糊化过程涉及从清晰量到模糊量的转换。在许多工程应用中,需要对结果或“模糊结果”进行去模糊化,以便将其转换为清晰结果。在数学上,去模糊化过程也称为“四舍五入”。
下面描述了不同的去模糊化方法:
最大隶属度法
该方法仅限于峰值输出函数,也称为高度法。在数学上,它可以表示如下:
$$\mu _{\widetilde{A}}\left ( x^* \right )>\mu _{\widetilde{A}}\left ( x \right ) \: 对所有 \:x \in X$$
这里,$x^*$是去模糊化后的输出。
质心法
该方法也称为面积中心法或重心法。在数学上,去模糊化后的输出$x^*$将表示为:
$$x^* = \frac{\int \mu _{\widetilde{A}}\left ( x \right ).xdx}{\int \mu _{\widetilde{A}}\left ( x \right ).dx}$$
加权平均法
在这种方法中,每个隶属函数都按其最大隶属度加权。在数学上,去模糊化后的输出$x^*$将表示为:
$$x^* = \frac{\sum \mu _{\widetilde{A}}\left ( \overline{x_i} \right ).\overline{x_i}}{\sum \mu _{\widetilde{A}}\left ( \overline{x_i} \right )}$$
平均最大隶属度法
该方法也称为最大值的中点法。在数学上,去模糊化后的输出$x^*$将表示为:
$$x^* = \frac{\displaystyle \sum_{i=1}^{n}\overline{x_i}}{n}$$
模糊逻辑 - 传统模糊知识回顾
逻辑最初只是研究区分可靠论证和不可靠论证的学科,如今已发展成为一个强大而严谨的体系,可以通过已知为真的其他陈述来发现真实的陈述。
谓词逻辑
这种逻辑处理谓词,谓词是包含变量的命题。
谓词是在某个特定域上定义的一个或多个变量的表达式。通过为变量赋值或对变量进行量化,可以将包含变量的谓词变成命题。
以下是一些谓词示例:
- 令 E(x, y) 表示 "x = y"
- 令 X(a, b, c) 表示 "a + b + c = 0"
- 令 M(x, y) 表示 "x 与 y 结婚"
命题逻辑
命题是由声明性语句组成的集合,这些语句具有真值“真”或真值“假”。命题由命题变量和连接词组成。命题变量用大写字母(A、B 等)表示。连接词连接命题变量。
以下是一些命题示例:
- "人是凡人",其真值为“真”
- "12 + 9 = 3 – 2",其真值为“假”
以下不是命题:
"A 小于 2" − 因为除非我们给 A 一个特定的值,否则我们无法判断该陈述是真还是假。
连接词
在命题逻辑中,我们使用以下五个连接词:
- 或 (∨)
- 与 (∧)
- 非/否定 (¬)
- 蕴涵/如果-那么 (→)
- 当且仅当 (⇔)
或 (∨)
两个命题 A 和 B 的或运算(写成 A∨B)如果命题变量 A 或 B 中至少有一个为真,则结果为真。
真值表如下:
| A | B | A ∨ B |
|---|---|---|
| 真 | 真 | 真 |
| 真 | 假 | 真 |
| 假 | 真 | 真 |
| 假 | 假 | 假 |
与 (∧)
两个命题 A 和 B 的与运算(写成 A∧B)如果命题变量 A 和 B 都为真,则结果为真。
真值表如下:
| A | B | A ∧ B |
|---|---|---|
| 真 | 真 | 真 |
| 真 | 假 | 假 |
| 假 | 真 | 假 |
| 假 | 假 | 假 |
否定 (¬)
命题 A 的否定(写成 ¬A)当 A 为真时为假,当 A 为假时为真。
真值表如下:
| A | ¬A |
|---|---|
| 真 | 假 |
| 假 | 真 |
蕴涵/如果-那么 (→)
蕴涵 A→B 是命题“如果 A,那么 B”。如果 A 为真而 B 为假,则结果为假。其余情况为真。
真值表如下:
| A | B | A→B |
|---|---|---|
| 真 | 真 | 真 |
| 真 | 假 | 假 |
| 假 | 真 | 真 |
| 假 | 假 | 真 |
当且仅当 (⇔)
A⇔B 是一个双条件逻辑连接词,当 p 和 q 相同(即两者都为假或两者都为真)时为真。
真值表如下:
| A | B | A⇔B |
|---|---|---|
| 真 | 真 | 真 |
| 真 | 假 | 假 |
| 假 | 真 | 假 |
| 假 | 假 | 真 |
良构公式
良构公式 (wff) 是满足以下条件之一的谓词:
- 所有命题常量和命题变量都是良构公式。
- 如果 x 是一个变量,而 Y 是一个良构公式,则 ∀xY 和 ∃xY 也是良构公式。
- 真值和假值是良构公式。
- 每个原子公式都是良构公式。
- 所有连接良构公式的连接词都是良构公式。
量词
谓词的变量由量词量化。谓词逻辑中有两种类型的量词:
- 全称量词
- 存在量词
全称量词
全称量词指出其范围内的语句对于特定变量的每个值都为真。它用符号 ∀ 表示。
∀xP(x) 读作对于 x 的每个值,P(x) 都为真。
示例 − “人是凡人”可以转换为命题形式 ∀xP(x)。这里,P(x) 是表示 x 是凡人的谓词,论域是所有的人。
存在量词
存在量词指出其范围内的语句对于特定变量的某些值都为真。它用符号 ∃ 表示。
∃xP(x) 读作对于 x 的某些值,P(x) 为真。
示例 − “有些人是不诚实的”可以转换为命题形式 ∃x P(x),其中 P(x) 是表示 x 不诚实的谓词,论域是某些人。
嵌套量词
如果我们使用的量词出现在另一个量词的范围内,则称为嵌套量词。
例子
- ∀ a∃bP(x,y),其中 P(a,b) 表示 a+b = 0
- ∀ a∀b∀cP(a,b,c),其中 P(a,b) 表示 a+(b+c) = (a+b)+c
注意 − ∀a∃bP(x,y) ≠ ∃a∀bP(x,y)
模糊逻辑 - 近似推理
以下是近似推理的不同模式:
范畴推理
在这种近似推理模式中,假设不包含模糊量词和模糊概率的前件采用规范形式。
定性推理
在这种近似推理模式中,前件和后件具有模糊语言变量;系统的输入-输出关系表示为模糊 IF-THEN 规则的集合。这种推理主要用于控制系统分析。
三段论推理
在这种近似推理模式中,包含模糊量词的前件与推理规则相关。它表示为:
x = S1A 是 B
y = S2C 是 D
------------------------
z = S3E 是 F
这里 A、B、C、D、E、F 是模糊谓词。
S1 和 S2 是给定的模糊量词。
S3 是需要确定的模糊量词。
性情推理
在这种近似推理模式中,前件是可能包含模糊量词“通常”的性情。量词通常将性情推理和三段论推理联系起来;因此它起着重要的作用。
例如,性情推理中的投影推理规则可以表示如下:
通常( (L,M) 是 R ) ⇒ 通常 (L 是 [R ↓ L])
这里[R ↓ L] 是模糊关系R在L上的投影
模糊逻辑规则库
众所周知,人类总是习惯于用自然语言进行交流。可以用以下自然语言表达式来表示人类知识:
如果 前件 那么 后件
如上所述的表达式称为模糊 IF-THEN 规则库。
规范形式
以下是模糊逻辑规则库的规范形式:
规则 1 − 如果条件 C1,则限制 R1
规则 2 − 如果条件 C1,则限制 R2
.
.
.
规则 n − 如果条件 C1,则限制 Rn
模糊 IF-THEN 规则的解释
模糊 IF-THEN 规则可以用以下四种形式解释:
赋值语句
这类语句使用“=”(等于号)进行赋值。它们具有以下形式:
a = hello
climate = summer
条件语句
这类语句使用“IF-THEN”规则库形式进行条件判断。它们具有以下形式:
如果温度很高,那么气候就炎热
如果食物新鲜,那么就吃。
无条件语句
它们具有以下形式:
GOTO 10
关闭风扇
语言变量
我们已经学习到模糊逻辑使用语言变量,语言变量是自然语言中的单词或句子。例如,如果我们说温度,它就是一个语言变量;它的值可以是很热或很冷,稍微热或稍微冷,很温暖,稍微温暖等等。单词“很”、“稍微”是语言修饰词。
语言变量的特征
以下四个术语表征语言变量:
- 变量名称,通常用 x 表示。
- 变量的术语集,通常用 t(x) 表示。
- 生成变量 x 值的句法规则。
- 将 x 的每个值与其意义联系起来的语义规则。
模糊逻辑中的命题
我们知道命题是用任何语言表达的句子,通常以以下规范形式表达:
s 为 P
这里,s 是主语,P 是谓语。
例如,“德里是印度的首府”,这是一个命题,其中“德里”是主语,“是印度的首府”是谓语,它显示了主语的属性。
我们知道逻辑是推理的基础,模糊逻辑通过在模糊命题中使用模糊谓词、模糊谓词修饰词、模糊量词和模糊限定词来扩展推理能力,这与经典逻辑不同。
模糊逻辑中的命题包括以下内容:
模糊谓词
自然语言中几乎每个谓词都是模糊的,因此,模糊逻辑具有诸如高、矮、温暖、热、快等谓词。
模糊谓词修饰词
我们在上面讨论了语言修饰词;我们还有许多模糊谓词修饰词充当修饰词。它们对于生成语言变量的值至关重要。例如,单词“很”、“稍微”是修饰词,命题可以是“水稍微热”。
模糊量词
它可以定义为一个模糊数,它对一个或多个模糊或非模糊集合的基数进行模糊分类。它可以用来影响模糊逻辑中的概率。例如,单词“许多”、“大多数”、“频繁”用作模糊量词,命题可以是“大多数人对此过敏”。
模糊限定词
现在让我们了解模糊限定词。模糊限定词也是模糊逻辑的命题。模糊限定具有以下形式:
基于真值的模糊限定
它声明模糊命题的真值程度。
表达式 − 它表示为x 是 t。这里,t 是模糊真值。
示例 − (汽车是黑色的)不是非常正确。
基于概率的模糊限定
它声明模糊命题的概率,无论是数值还是区间。
表达式 − 它表示为x 是 λ。这里,λ 是模糊概率。
示例 − (汽车是黑色的)可能是。
基于可能性的模糊限定
它声明模糊命题的可能性。
表达式 − 它表示为x 是 π。这里,π 是模糊可能性。
示例 − (汽车是黑色的)几乎不可能。
模糊逻辑 - 推理系统
模糊推理系统是模糊逻辑系统的一个关键单元,其主要工作是决策。它使用“IF…THEN”规则以及连接词“OR”或“AND”来制定必要的决策规则。
模糊推理系统的特性
以下是 FIS 的一些特性:
无论输入是模糊的还是清晰的,FIS 的输出始终是模糊集。
当用作控制器时,需要模糊输出。
FIS 将配备一个去模糊单元,用于将模糊变量转换为清晰变量。
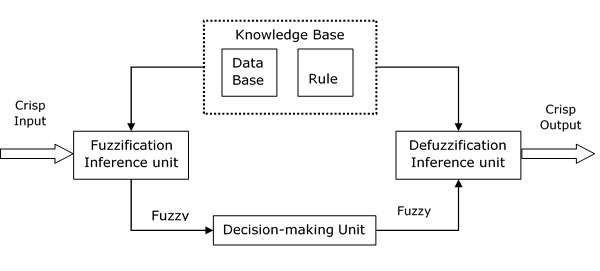
FIS 的功能模块
以下五个功能模块将帮助您了解 FIS 的构建:
规则库 − 它包含模糊 IF-THEN 规则。
数据库 − 它定义模糊规则中使用的模糊集的隶属函数。
决策单元 − 它对规则进行运算。
模糊化接口单元 − 它将清晰量转换为模糊量。
去模糊化接口单元 − 它将模糊量转换为清晰量。以下是模糊干扰系统的框图。
FIS 的工作原理
FIS 的工作原理包括以下步骤:
模糊化单元支持多种模糊化方法的应用,并将清晰输入转换为模糊输入。
在将清晰输入转换为模糊输入后,形成知识库——规则库和数据库的集合。
去模糊单元将模糊输入最终转换为清晰输出。
FIS 的方法
现在让我们讨论 FIS 的不同方法。以下是 FIS 的两种重要方法,它们具有不同的模糊规则结果:
- Mamdani 模糊推理系统
- Takagi-Sugeno 模糊模型 (TS 方法)
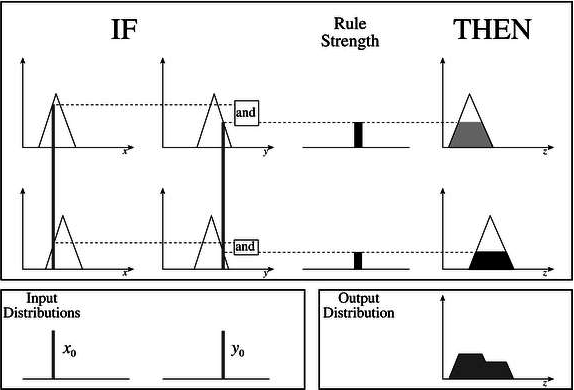
Mamdani 模糊推理系统
该系统由Ebrahim Mamdani于1975年提出。其基本思想是通过综合从系统操作人员那里获得的一组模糊规则来控制蒸汽机和锅炉组合。
输出计算步骤
要从该模糊推理系统(FIS)计算输出,需要遵循以下步骤:
步骤1 − 此步骤需要确定模糊规则集。
步骤2 − 此步骤使用输入隶属函数将输入模糊化。
步骤3 − 现在根据模糊规则,结合模糊化后的输入来建立规则强度。
步骤4 − 此步骤通过结合规则强度和输出隶属函数来确定规则的结果。
步骤5 − 将所有结果结合起来以获得输出分布。
步骤6 − 最后,获得去模糊化的输出分布。
以下是Mamdani模糊接口系统的框图。(此处应插入框图)
Takagi-Sugeno 模糊模型 (TS 方法)
该模型由Takagi、Sugeno和Kang于1985年提出。规则格式如下:
如果x是A且y是B,则Z = f(x,y)
这里,A和B是前件中的模糊集,z = f(x,y)是结果中的精确函数。
模糊推理过程
Takagi-Sugeno模糊模型(TS方法)下的模糊推理过程按以下方式进行:
步骤1:模糊化输入 − 此处,将系统的输入模糊化。
步骤2:应用模糊算子 − 此步骤必须应用模糊算子以获得输出。
Sugeno形式的规则格式
Sugeno形式的规则格式如下:
如果7 = x且9 = y,则输出为z = ax+by+c
两种方法的比较
现在让我们了解Mamdani系统和Sugeno模型之间的比较。
输出隶属函数 − 两者之间的主要区别在于输出隶属函数的基础上。Sugeno输出隶属函数是线性的或常数的。
聚合和去模糊化过程 − 两者之间的区别还在于模糊规则的结果,并且由于相同的原因,它们的聚合和去模糊化过程也不同。
数学规则 − Sugeno规则比Mamdani规则具有更多数学规则。
可调参数 − Sugeno控制器比Mamdani控制器具有更多可调参数。
模糊逻辑 - 数据库和查询
我们在之前的章节中学习过,模糊逻辑是一种基于“真值程度”而不是通常的“真或假”逻辑的计算方法。它处理的是近似的而不是精确的推理,以一种更类似于人类逻辑的方式解决问题,因此,布尔代数的二值实现数据库查询过程是不够的。
数据库上关系的模糊场景
可以通过以下示例来理解数据库上关系的模糊场景:
例子
假设我们有一个数据库,其中包含访问过印度的人员记录。在简单的数据库中,我们将以以下方式进行条目:
| 姓名 | 年龄 | 国籍 | 访问国家 | 停留天数 | 访问年份 |
|---|---|---|---|---|---|
| John Smith | 35 | 美国 | 印度 | 41 | 1999 |
| John Smith | 35 | 美国 | 意大利 | 72 | 1999 |
| John Smith | 35 | 美国 | 日本 | 31 | 1999 |
现在,如果有人查询99年访问过印度和日本并且是美国公民的人,则输出将显示两条包含John Smith姓名条目的记录。这是一个简单的查询,生成简单的输出。
但是,如果我们想知道上述查询中的人是否年轻呢?根据上述结果,该人的年龄为35岁。但是,我们可以假设此人年轻还是不年轻呢?同样,相同的事情也可以应用于其他字段,如停留天数、访问年份等。
可以使用模糊值集来解决上述问题,如下所示:
FV(年龄){非常年轻,年轻,有点老,老}
FV(停留天数){几乎几天,几天,相当几天,许多天}
FV(访问年份){遥远的过去,最近的过去,最近}
现在,如果任何查询具有模糊值,则结果也将具有模糊性。
模糊查询系统
模糊查询系统是一个用户界面,用于使用(准)自然语言句子从数据库获取信息。已经提出了许多模糊查询实现,导致略微不同的语言。尽管根据不同实现的特殊性存在一些差异,但模糊查询句子的答案通常是按匹配程度排序的记录列表。
模糊逻辑 - 量化
在对自然语言语句建模时,量化语句起着重要作用。这意味着自然语言很大程度上依赖于量化结构,而量化结构通常包括模糊概念,如“几乎所有”、“许多”等。以下是量化命题的一些示例:
- 每个学生都通过了考试。
- 每辆跑车都很贵。
- 许多学生通过了考试。
- 许多跑车都很贵。
在上述示例中,量词“每个”和“许多”应用于清晰的限制“学生”以及清晰的范围“(通过考试的)人”和“汽车”以及清晰的范围“跑车”。
模糊事件、模糊均值和模糊方差
借助一个例子,我们可以理解上述概念。让我们假设我们是名为ABC公司的股东。目前,该公司每股股票售价为40卢比。还有三家业务与ABC类似的公司,但它们以不同的价格提供股票——每股100卢比、每股85卢比和每股60卢比。
现在,这种价格收购的概率分布如下:
| 价格 | 100卢比 | 85卢比 | 60卢比 |
|---|---|---|---|
| 概率 | 0.3 | 0.5 | 0.2 |
(此处应插入概率值)
100 × 0.3 + 85 × 0.5 + 60 × 0.2 = 84.5
并且,根据标准概率论,上述分布给出的预期价格方差如下:
(100 − 84.5)² × 0.3 + (85 − 84.5)² × 0.5 + (60 − 84.5)² × 0.2 = 124.825
假设100在这个集合中的隶属度为0.7,85的隶属度为1,60的隶属度为0.5。这些可以反映在以下模糊集中:
$$ \left \{ \frac{0.7}{100}, \: \frac{1}{85}, \: \frac{0.5}{60} \right \} $$
以这种方式获得的模糊集称为模糊事件。
我们想要模糊事件的概率,我们的计算结果为:
0.7 × 0.3 + 1 × 0.5 + 0.5 × 0.2 = 0.21 + 0.5 + 0.1 = 0.81
现在,我们需要计算模糊均值和模糊方差,计算如下:
模糊均值 $= \left ( \frac{1}{0.81} \right ) × (100 × 0.7 × 0.3 + 85 × 1 × 0.5 + 60 × 0.5 × 0.2)$
$= 85.8$
模糊方差 $= 7496.91 − 7361.91 = 135.27$ (这个计算过程似乎有问题,需要核实)
模糊逻辑 - 决策
这是一种活动,其中包括为实现某个目标而需要采取的步骤,以从那些需要的替代方案中选择合适的替代方案。
决策步骤
现在让我们讨论决策过程中涉及的步骤:
确定备选方案集 − 此步骤必须确定需要从中做出决策的备选方案。
评估备选方案 − 在这里,必须评估备选方案,以便可以就其中一个备选方案做出决策。
比较备选方案 − 此步骤对评估的备选方案进行比较。
决策类型
现在我们将了解不同类型的决策。
个人决策
在这种类型的决策中,只有一人负责做出决策。在这种情况下,决策模型可以描述为:
可能的行动集
目标集 $G_i\left ( i \: \in \: X_n \right );$
约束集 $C_j\left ( j \: \in \: X_m \right )$
上述目标和约束用模糊集表示。
现在考虑集合A。那么,该集合的目标和约束由下式给出:
$G_i\left ( a \right )$ = 复合 $\left [ G_i\left ( a \right ) \right ]$ = $G_i^1\left ( G_i\left ( a \right ) \right )$ with $G_i^1$
$C_j\left ( a \right )$ = 复合 $\left [ C_j\left ( a \right ) \right ]$ = $C_j^1\left ( C_j\left ( a \right ) \right )$ with $C_j^1$ 对于 $a\:\in \:A$
上述情况下的模糊决策由下式给出:
$$F_D = min[i\in X_{n}^{in}fG_i\left ( a \right ),j\in X_{m}^{in}fC_j\left ( a \right )]$$
多人决策
在这种情况下,决策包括几个人,以便利用不同人的专业知识来做出决策。
计算如下:
偏好 $x_i$ 而不是 $x_j$ 的人数 = $N\left ( x_i, \: x_j \right )$
决策者总数 = $n$
然后,$SC\left ( x_i, \: x_j \right ) = \frac{N\left ( x_i, \: x_j \right )}{n}$
多目标决策
当存在多个要实现的目标时,就会发生多目标决策。这种类型的决策有两个问题:
获取与各种备选方案对目标满意度的相关信息。
权衡每个目标的相对重要性。
在数学上,我们可以定义一个n个备选方案的集合为:
$A = \left [ a_1, \:a_2,\:..., \: a_i, \: ..., \:a_n \right ]$
以及“m”个目标的集合为 $O = \left [ o_1, \:o_2,\:..., \: o_i, \: ..., \:o_n \right ]$
多属性决策
当可以基于对象的多个属性来进行备选方案的评估时,就会进行多属性决策。属性可以是数值数据、语言数据和定性数据。
在数学上,多属性评估是基于以下线性方程进行的:
$$Y = A_1X_1+A_2X_2+...+A_iX_i+...+A_rX_r$$
模糊逻辑 - 控制系统
模糊逻辑在各种控制应用中都取得了巨大的成功。几乎所有消费产品都具有模糊控制。一些例子包括使用空调控制室温、车辆中使用的防抱死系统、交通灯控制、洗衣机、大型经济系统等。
为什么在控制系统中使用模糊逻辑
控制系统是由物理组件组成的装置,旨在改变另一个物理系统,以便该系统表现出某些期望的特性。以下是在控制系统中使用模糊逻辑的一些原因:
在应用传统控制时,需要了解以精确术语制定的模型和目标函数。这使得在许多情况下很难应用。
通过应用模糊逻辑控制,我们可以利用人类的专业知识和经验来设计控制器。
模糊控制规则,基本上就是IF-THEN规则,可以最好地用于设计控制器。
模糊逻辑控制 (FLC) 设计中的假设
在设计模糊控制系统时,应做出以下六个基本假设:
系统是可观测的和可控的 − 必须假设输入、输出以及状态变量都可用于观测和控制。
知识库的存在 − 必须假设存在一个知识库,其中包含语言规则和一组可以从中提取规则的输入输出数据集。
解的存在性 − 必须假设存在解。
“足够好”的解就足够了 − 控制工程应该寻找“足够好”的解,而不是最优解。
精度范围 − 模糊逻辑控制器必须设计在可接受的精度范围内。
关于稳定性和最优性的问题 − 在设计模糊逻辑控制器时,稳定性和最优性的问题必须是开放的,而不是明确解决的。
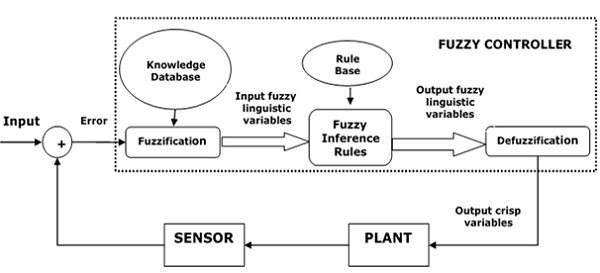
模糊逻辑控制的架构
下图显示了模糊逻辑控制 (FLC) 的架构。
FLC 的主要组成部分
以下是上图所示 FLC 的主要组成部分:
模糊化器 − 模糊化器的作用是将清晰的输入值转换为模糊值。
模糊知识库 − 它存储有关所有输入输出模糊关系的知识。它还具有隶属函数,该函数将输入变量定义为模糊规则库,将输出变量定义为被控对象。
模糊规则库 − 它存储有关过程或领域操作的知识。
推理引擎 − 它是任何 FLC 的核心。它基本上通过执行近似推理来模拟人类决策。
反模糊化器 − 反模糊化器的作用是从模糊推理引擎获得模糊值并将其转换为清晰值。
FLC 设计步骤
以下是 FLC 设计中涉及的步骤:
变量识别 − 在这里,必须识别所考虑对象的输入、输出和状态变量。
模糊子集配置 − 将信息宇宙划分为多个模糊子集,并为每个子集分配一个语言标签。务必确保这些模糊子集包含宇宙的所有元素。
获取隶属函数 − 现在为我们在上述步骤中获得的每个模糊子集获得隶属函数。
模糊规则库配置 − 现在通过分配模糊输入和输出之间的关系来制定模糊规则库。
模糊化 − 此步骤启动模糊化过程。
组合模糊输出 − 通过应用模糊近似推理,找到模糊输出并将其合并。
反模糊化 − 最后,启动反模糊化过程以形成清晰的输出。
模糊逻辑控制的优点
现在让我们讨论模糊逻辑控制的优点。
更便宜 − 就性能而言,开发 FLC 比开发基于模型的控制器或其他控制器便宜。
鲁棒性 − 由于 FLC 能够覆盖很大的运行条件范围,因此它们比 PID 控制器更鲁棒。
可定制性 − FLC 是可定制的。
模拟人类演绎思维 − FLC 的基本设计是模拟人类演绎思维,即人们用来从已知信息中推断结论的过程。
可靠性 − FLC 比传统的控制系统更可靠。
效率 − 模糊逻辑应用于控制系统时效率更高。
模糊逻辑控制的缺点
我们现在将讨论模糊逻辑控制的缺点。
需要大量数据 − FLC 需要大量数据才能应用。
适用于中等历史数据的情况 − FLC 不适用于远小于或远大于历史数据的程序。
需要很高的专业知识 − 这是一个缺点,因为系统的准确性取决于人类的知识和专业知识。
需要定期更新规则 − 规则必须随着时间的推移而更新。
自适应模糊控制器
本章将讨论什么是自适应模糊控制器及其工作原理。自适应模糊控制器设计了一些可调参数以及用于调整它们的嵌入式机制。自适应控制器已被用于提高控制器的性能。
实施自适应算法的基本步骤
现在让我们讨论实施自适应算法的基本步骤。
收集可观测数据 − 收集可观测数据以计算控制器的性能。
调整控制器参数 − 现在,借助控制器性能,将计算控制器参数的调整。
提高控制器性能 − 在此步骤中,调整控制器参数以提高控制器的性能。
操作概念
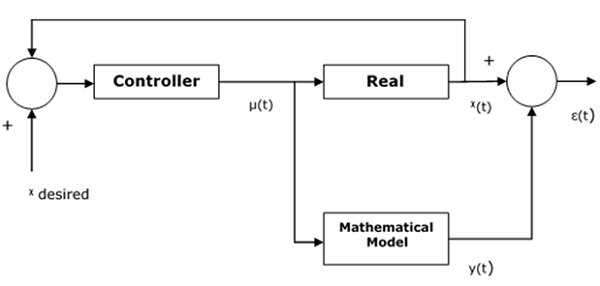
控制器的设计基于一个模拟真实系统的假设数学模型。计算实际系统与其数学表示之间的误差,如果误差相对较小,则认为该模型有效。
还存在一个阈值常数,它为控制器的有效性设置一个边界。控制输入被送入真实系统和数学模型。这里,假设 $x\left ( t \right )$ 是真实系统的输出,$y\left ( t \right )$ 是数学模型的输出。然后可以计算误差 $\epsilon \left ( t \right )$ 如下:
$$\epsilon \left ( t \right ) = x\left ( t \right ) - y\left ( t \right )$$
这里,$x_{desired}$ 是我们想要从系统中获得的输出,$\mu \left ( t \right )$ 是来自控制器并进入真实系统和数学模型的输出。
下图显示了如何跟踪真实系统输出和数学模型之间的误差函数:
系统的参数化
基于模糊数学模型设计的模糊控制器将具有以下形式的模糊规则:
规则 1 − IF $x_1\left ( t_n \right )\in X_{11} \: AND...AND\: x_i\left ( t_n \right )\in X_{1i}$
THEN $\mu _1\left ( t_n \right ) = K_{11}x_1\left ( t_n \right ) + K_{12}x_2\left ( t_n \right ) \: +...+ \: K_{1i}x_i\left ( t_n \right )$
规则 2 − IF $x_1\left ( t_n \right )\in X_{21} \: AND...AND \: x_i\left ( t_n \right )\in X_{2i}$
THEN $\mu _2\left ( t_n \right ) = K_{21}x_1\left ( t_n \right ) + K_{22}x_2\left ( t_n \right ) \: +...+ \: K_{2i}x_i\left ( t_n \right ) $
.
.
.
规则 j − IF $x_1\left ( t_n \right )\in X_{k1} \: AND...AND \: x_i\left ( t_n \right )\in X_{ki}$
THEN $\mu _j\left ( t_n \right ) = K_{j1}x_1\left ( t_n \right ) + K_{j2}x_2\left ( t_n \right ) \: +...+ \: K_{ji}x_i\left ( t_n \right ) $
上述参数集表征了控制器。
机制调整
调整控制器参数以提高控制器的性能。计算参数调整的过程是调整机制。
数学上,令 $\theta ^\left ( n \right )$ 为在时间 $t = t_n$ 时要调整的参数集。调整可以是参数的重新计算,
$$\theta ^\left ( n \right ) = \Theta \left ( D_0,\: D_1, \: ..., \:D_n \right )$$
这里 $D_n$ 是在时间 $t = t_n$ 收集的数据。
现在,通过基于其先前值更新参数集来重新制定此公式,
$$\theta ^\left ( n \right ) = \phi ( \theta ^{n-1}, \: D_n)$$
选择自适应模糊控制器的参数
选择自适应模糊控制器需要考虑以下参数:
系统能否完全由模糊模型逼近?
如果系统可以完全由模糊模型逼近,则该模糊模型的参数是否容易获得,或者必须在线确定?
如果系统不能完全由模糊模型逼近,它能否由一组模糊模型分段逼近?
如果系统可以由一组模糊模型逼近,这些模型是否具有相同的格式但参数不同,或者它们具有不同的格式?
如果系统可以由一组具有相同格式的模糊模型逼近,每个模型都有一组不同的参数,则这些参数集是否容易获得,或者必须在线确定?
神经网络中的模糊性
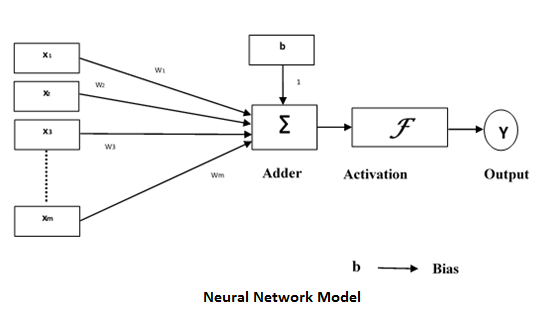
人工神经网络 (ANN) 是一个高效的计算系统网络,其核心主题借鉴了生物神经网络的类比。人工神经网络也称为“人工神经系统”、“并行分布式处理系统”、“连接主义系统”。人工神经网络获取大量单元,这些单元以某种模式互连,以允许单元之间进行通信。这些单元也称为节点或神经元,是并行工作的简单处理器。
每个神经元都通过连接链与其他神经元连接。每个连接链都与一个权重相关联,该权重包含有关输入信号的信息。这是神经元解决特定问题最有用的信息,因为权重通常会抑制正在传输的信号。每个神经元都有其内部状态,称为激活信号。在组合输入信号和激活规则后产生的输出信号可能会发送到其他单元。它还包括一个偏差“b”,其权重始终为 1。
为什么在神经网络中使用模糊逻辑
正如我们上面所讨论的,人工神经网络中的每个神经元都通过连接链与其他神经元连接,并且该链与一个包含有关输入信号信息的权重相关联。因此,我们可以说权重包含有关输入的有用信息以解决问题。
以下是神经网络中使用模糊逻辑的一些原因:
模糊逻辑主要用于在神经网络中从模糊集定义权重。
当无法应用清晰值时,使用模糊值。
我们已经学习过,训练和学习有助于神经网络在意外情况下表现更好。那时,模糊值比清晰值更适用。
当我们在神经网络中使用模糊逻辑时,值一定不能是清晰的,并且可以并行进行处理。
模糊认知图
它是一种神经网络中的模糊性形式。基本上,FCM就像一个具有模糊状态(不仅仅是1或0)的动态状态机。
在神经网络中使用模糊逻辑的困难
尽管具有众多优点,但在神经网络中使用模糊逻辑时也存在一些困难。困难与隶属度规则有关,需要构建模糊系统,因为有时很难根据给定的复杂数据集推导出它。
神经网络训练的模糊逻辑
神经网络和模糊逻辑之间的反向关系,即使用神经网络训练模糊逻辑也是一个很好的研究领域。以下是构建神经网络训练的模糊逻辑的两个主要原因:
借助神经网络可以轻松学习新的数据模式,因此可以用于预处理模糊系统中的数据。
神经网络由于其能够学习新的输入数据的新关系的能力,可以用来改进模糊规则以创建模糊自适应系统。
神经网络训练的模糊系统的示例
神经网络训练的模糊系统正在许多商业应用中使用。让我们看看一些应用神经网络训练的模糊系统的例子:
位于日本横滨的国际模糊工程研究实验室 (LIFE) 拥有一个反向传播神经网络,可以推导出模糊规则。该系统已成功应用于外汇交易系统,大约有 5000 条模糊规则。
福特汽车公司已经开发出用于汽车怠速控制的可训练模糊系统。
国家半导体公司的软件产品 NeuFuz 支持使用神经网络为控制应用生成模糊规则。
德国的 AEG 公司在其节水节能机器中使用神经网络训练的模糊控制系统。它共有 157 条模糊规则。
模糊逻辑 - 应用
在本章中,我们将讨论模糊逻辑概念被广泛应用的领域。
航空航天
在航空航天领域,模糊逻辑用于以下领域:
- 航天器的姿态控制
- 卫星高度控制
- 飞机除冰车辆中的流量和混合物调节
汽车
在汽车领域,模糊逻辑用于以下领域:
- 用于怠速控制的可训练模糊系统
- 自动变速器的换档调度方法
- 智能高速公路系统
- 交通控制
- 提高自动变速器的效率
商业
在商业领域,模糊逻辑用于以下领域:
- 决策支持系统
- 大公司的人员评估
国防
在国防领域,模糊逻辑用于以下领域:
- 水下目标识别
- 热红外图像的自动目标识别
- 海军决策支持工具
- 超高速拦截器的控制
- 北约决策的模糊集建模
电子
在电子领域,模糊逻辑用于以下领域:
- 控制摄像机的自动曝光
- 洁净室的湿度控制
- 空调系统
- 洗衣机定时
- 微波炉
- 真空吸尘器
金融
在金融领域,模糊逻辑用于以下领域:
- 钞票转账控制
- 资金管理
- 股市预测
工业部门
在工业领域,模糊逻辑用于以下领域:
- 水泥窑控制、热交换器控制
- 活性污泥污水处理过程控制
- 水净化厂控制
- 工业质量保证的定量模式分析
- 结构设计中约束满足问题的控制
- 水净化厂控制
制造业
在制造业中,模糊逻辑用于以下领域:
- 奶酪生产优化
- 牛奶生产优化
海洋
在海洋领域,模糊逻辑用于以下领域:
- 船舶自动驾驶仪
- 最佳航线选择
- 自主水下航行器的控制
- 船舶操纵
医疗
在医疗领域,模糊逻辑用于以下领域:
- 医疗诊断支持系统
- 麻醉期间动脉压力的控制
- 麻醉的多变量控制
- 阿尔茨海默病患者神经病理学发现的建模
- 放射学诊断
- 糖尿病和前列腺癌的模糊推理诊断
证券
在证券领域,模糊逻辑用于以下领域:
- 证券交易决策系统
- 各种安全设备
交通运输
在交通运输领域,模糊逻辑用于以下领域:
- 自动地下列车运行
- 列车时刻表控制
- 铁路加速
- 制动和停车
模式识别与分类
在模式识别与分类中,模糊逻辑用于以下领域:
- 基于模糊逻辑的语音识别
- 基于模糊逻辑的
- 手写识别
- 基于模糊逻辑的面部特征分析
- 命令分析
- 模糊图像搜索
心理学
在心理学领域,模糊逻辑用于以下领域:
- 基于模糊逻辑的人类行为分析
- 基于模糊逻辑推理的犯罪调查和预防