模糊逻辑 - 经典集合论

---

---

集合是不同元素的无序集合。它可以通过使用集合括号列出其元素来明确表示。如果元素的顺序发生变化或集合的任何元素重复，则不会对集合进行任何更改。

示例

• 所有正整数的集合。
• 太阳系中所有行星的集合。
• 印度所有邦的集合。
• 字母表中所有小写字母的集合。

集合的数学表示

集合可以用两种方式表示：

列举法或表格法

在这种形式中，集合通过列出构成它的所有元素来表示。元素用大括号括起来，并用逗号分隔。

以下是列举法或表格法表示集合的示例：

• 英语字母表中元音的集合，A = {a,e,i,o,u}
• 小于 10 的奇数集合，B = {1,3,5,7,9}

集合构建器表示法

在这种形式中，集合是通过指定集合元素共有的属性来定义的。集合描述为 A = {x:p(x)}

示例 1 - 集合 {a,e,i,o,u} 写成

A = {x:x 是英语字母表中的元音}

示例 2 - 集合 {1,3,5,7,9} 写成

B = {x:1 ≤ x < 10 且 (x%2) ≠ 0}

如果元素 x 是任何集合 S 的成员，则表示为 x∈S，如果元素 y 不是集合 S 的成员，则表示为 y∉S。

示例 - 如果 S = {1,1.2,1.7,2}，则 1 ∈ S 但 1.5 ∉ S

集合的基数

集合 S 的基数，表示为 |S|，是集合的元素个数。该数字也称为基数。如果一个集合有无限多个元素，则其基数为 ∞。

示例 - |{1,4,3,5}| = 4，|{1,2,3,4,5,…}| = ∞

如果有两个集合 X 和 Y，|X| = |Y| 表示两个集合 X 和 Y 具有相同的基数。当 X 中的元素数量正好等于 Y 中的元素数量时发生这种情况。在这种情况下，存在从 X 到 Y 的双射函数“f”。

|X| ≤ |Y| 表示集合 X 的基数小于或等于集合 Y 的基数。当 X 中的元素数量小于或等于 Y 中的元素数量时发生这种情况。在这里，存在从 X 到 Y 的单射函数“f”。

|X| < |Y| 表示集合 X 的基数小于集合 Y 的基数。当 X 中的元素数量小于 Y 中的元素数量时发生这种情况。在这里，从 X 到 Y 的函数“f”是单射函数但不是双射函数。

如果 |X| ≤ |Y| 和 |X| ≤ |Y| 则 |X| = |Y|。集合 X 和 Y 通常称为等价集合。

集合的类型

集合可以分为多种类型；其中一些是有限的、无限的、子集的、全集的、真子集的、单元素集的等等。

有限集

包含确定数量元素的集合称为有限集。

示例 - S = {x|x ∈ N 且 70 > x > 50}

无限集

包含无限多个元素的集合称为无限集。

示例 - S = {x|x ∈ N 且 x > 10}

子集

如果集合 X 的每个元素都是集合 Y 的元素，则集合 X 是集合 Y 的子集（写成 X ⊆ Y）。

示例 1 - 令 X = {1,2,3,4,5,6} 且 Y = {1,2}。这里集合 Y 是集合 X 的子集，因为集合 Y 的所有元素都在集合 X 中。因此，我们可以写成 Y⊆X。

示例 2 - 令 X = {1,2,3} 且 Y = {1,2,3}。这里集合 Y 是集合 X 的子集（不是真子集），因为集合 Y 的所有元素都在集合 X 中。因此，我们可以写成 Y⊆X。

真子集

术语“真子集”可以定义为“子集但不等”。如果集合 X 的每个元素都是集合 Y 的元素且 |X| < |Y|，则集合 X 是集合 Y 的真子集（写成 X ⊂ Y）。

示例 - 令 X = {1,2,3,4,5,6} 且 Y = {1,2}。这里集合 Y ⊂ X，因为 Y 中的所有元素都包含在 X 中，并且 X 至少有一个元素比集合 Y 多。

全集

它是特定上下文或应用程序中所有元素的集合。该上下文或应用程序中的所有集合本质上都是这个全集的子集。全集表示为 U。

示例 - 我们可以将 U 定义为地球上所有动物的集合。在这种情况下，所有哺乳动物的集合是 U 的子集，所有鱼类的集合是 U 的子集，所有昆虫的集合是 U 的子集，等等。

空集或零集

空集不包含任何元素。它用 Φ 表示。由于空集中的元素数量是有限的，因此空集是有限集。空集或零集的基数为零。

示例 – S = {x|x ∈ N 且 7 < x < 8} = Φ

单元素集或单元集

单元素集或单元集仅包含一个元素。单元素集表示为 {s}。

示例 - S = {x|x ∈ N，7 < x < 9} = {8}

相等集

如果两个集合包含相同的元素，则称它们相等。

示例 - 如果 A = {1,2,6} 且 B = {6,1,2}，则它们相等，因为集合 A 的每个元素都是集合 B 的元素，并且集合 B 的每个元素都是集合 A 的元素。

等价集

如果两个集合的基数相同，则称为等价集合。

示例 - 如果 A = {1,2,6} 且 B = {16,17,22}，则它们是等价的，因为 A 的基数等于 B 的基数。即 |A| = |B| = 3

重叠集

至少有一个共同元素的两个集合称为重叠集。在重叠集的情况下 -

$$n\left ( A\cup B \right ) = n\left ( A \right ) + n\left ( B \right ) - n\left ( A\cap B \right )$$

$$n\left ( A\cup B \right ) = n\left ( A-B \right )+n\left ( B-A \right )+n\left ( A\cap B \right )$$

$$n\left ( A \right ) = n\left ( A-B \right )+n\left ( A\cap B \right )$$

$$n\left ( B \right ) = n\left ( B-A \right )+n\left ( A\cap B \right )$$

示例 - 令 A = {1,2,6} 且 B = {6,12,42}。有一个共同元素“6”，因此这些集合是重叠集。

不相交集

如果两个集合 A 和 B 没有任何共同元素，则称为不相交集。因此，不相交集具有以下性质 -

$$n\left ( A\cap B \right ) = \phi$$

$$n\left ( A\cup B \right ) = n\left ( A \right )+n\left ( B \right )$$

示例 - 令 A = {1,2,6} 且 B = {7,9,14}，没有一个共同元素，因此这些集合是重叠集。

经典集合上的运算

集合运算包括集合并、集合交、集合差、集合补和笛卡尔积。

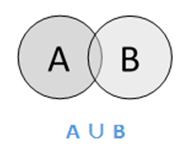
并集

集合 A 和 B 的并集（用 A ∪ B 表示）是 A 中、B 中或 A 和 B 中的元素的集合。因此，A ∪ B = {x|x ∈ A 或 x ∈ B}。

示例 - 如果 A = {10,11,12,13} 且 B = {13,14,15}，则 A ∪ B = {10,11,12,13,14,15} - 公共元素仅出现一次。

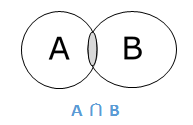
交集

集合 A 和 B 的交集（用 A ∩ B 表示）是 A 和 B 中的元素的集合。因此，A ∩ B = {x|x ∈ A 且 x ∈ B}。

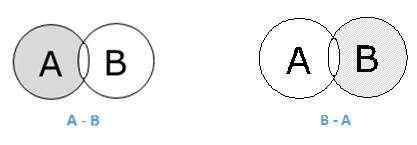
差集/相对补集

集合 A 和 B 的差集（用 A–B 表示）是仅在 A 中而不是在 B 中的元素的集合。因此，A − B = {x|x ∈ A 且 x ∉ B}。

示例 - 如果 A = {10,11,12,13} 且 B = {13,14,15}，则 (A − B) = {10,11,12} 且 (B − A) = {14,15}。在这里，我们可以看到 (A − B) ≠ (B − A)

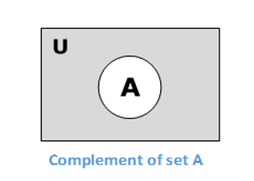
集合的补集

集合 A 的补集（用 A′ 表示）是不在集合 A 中的元素的集合。因此，A′ = {x|x ∉ A}。

更具体地说，A′ = (U−A)，其中 U 是包含所有对象的全集。

示例 - 如果 A = {x|x 属于奇整数集合}，则 A′ = {y|y 不属于奇整数集合}

笛卡尔积/叉积

n 个集合 A1、A2、…An 的笛卡尔积表示为 A1 × A2...× An，可以定义为所有可能的序偶 (x1,x2,…xn)，其中 x1 ∈ A1、x2 ∈ A2、…xn ∈ An

示例 - 如果我们取两个集合 A = {a,b} 和 B = {1,2}，

A 和 B 的笛卡尔积写成 - A × B = {(a,1),(a,2),(b,1),(b,2)}

并且，B 和 A 的笛卡尔积写成 - B × A = {(1,a),(1,b),(2,a),(2,b)}

经典集合的性质

集合的性质在获得解方面起着重要作用。以下是经典集合的不同性质 -

交换律

有两个集合A和B，此属性指出 -

$$A \cup B = B \cup A$$

$$A \cap B = B \cap A$$

结合律

有三个集合A、B和C，此属性指出 -

$$A\cup \left ( B\cup C \right ) = \left ( A\cup B \right )\cup C$$

$$A\cap \left ( B\cap C \right ) = \left ( A\cap B \right )\cap C$$

分配律

有三个集合A、B和C，此属性指出 -

$$A\cup \left ( B\cap C \right ) = \left ( A\cup B \right )\cap \left ( A\cup C \right )$$

$$A\cap \left ( B\cup C \right ) = \left ( A\cap B \right )\cup \left ( A\cap C \right )$$

幂等律（Idempotency Property）

对于任意集合A，该性质陈述如下：

$$A\cup A = A$$

$$A\cap A = A$$

恒等律（Identity Property）

对于集合A和全集X，该性质陈述如下：

$$A\cup \varphi = A$$

$$A\cap X = A$$

$$A\cap \varphi = \varphi$$

$$A\cup X = X$$

传递律（Transitive Property）

对于三个集合A、B和C，该性质陈述如下：

如果 $A\subseteq B\subseteq C$，则 $A\subseteq C$

对合律（Involution Property）

对于任意集合A，该性质陈述如下：

$$\overline{{\overline{A}}} = A$$

德摩根定律（De Morgan’s Law）

这是一个非常重要的定律，有助于证明重言式和矛盾。该定律陈述如下：

$$\overline{A\cap B} = \overline{A} \cup \overline{B}$$

$$\overline{A\cup B} = \overline{A} \cap \overline{B}$$