设ABC为一个直角三角形，其中AB = 6厘米，BC = 8厘米，∠B = 90°。BD是B到AC的垂线。作过B、C、D三点的圆。作从A到这个圆的切线。

已知

一个直角三角形ABC，其中AB = 6厘米，BC = 8厘米，∠B = 90°。

要求

我们必须从A点作这个圆的切线。

解法

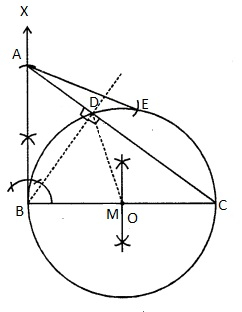
作图步骤

(i) 画一条线段BC = 8厘米。

(ii) 从B点画一个90°角。

(iii) 画一条弧BA = 6厘米，与角相交于A点。

(iv) 连接AC。ABC是所需的三角形。

(v) 画BC的垂直平分线，与BC相交于M点。

(vi) 以M为圆心，BM为半径画一个圆。

(vii) 以A为圆心，AB为半径画一条弧，与圆相交于E点。连接AE。

AB和AE是所需的切线。

证明

∠ABC = 90° (已知)

OB是圆的半径。

这意味着：

AB是圆的切线。

同样，AE是圆的切线。

更新于：2022年10月10日

46 次浏览

开启您的职业生涯

完成课程获得认证

开始学习
广告