一个风筝，形状为正方形，对角线长 32 厘米，还有一个等腰三角形，底边长 8 厘米，两腰各长 6 厘米。风筝由三种不同的颜色制作而成，如图所示。每种颜色纸张的使用量是多少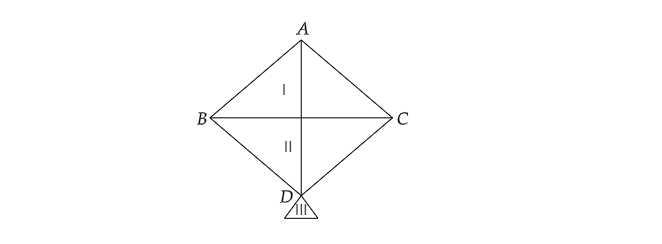？"\n

已知：

一个风筝，形状为正方形，对角线长 $32\ cm$，还有一个等腰三角形，底边长 $8\ cm$，两腰各长 $6\ cm$。风筝由三种不同的颜色制作而成，如图所示。

要求：

求每种颜色纸张的使用量。

解答

假设风筝由正方形 $ABCD$ 和等腰三角形 $\vartriangle DEF$ 组成。

已知，$\vartriangle DEF$ 的三条边长为 $DE=DF=6\ cm$ 和 $EF=8\ cm$，正方形 $ABCD$ 的对角线长为 $32\ cm$。

我们知道，

正方形的对角线互相平分且垂直。

$OA=OB=OC=OD=\frac{32}{2}=16\ cm$

$AO$ 垂直于 $BC$ 且 $DO$ 垂直于 $BC$。

区域 I 的面积 = $\vartriangle ABC$ 的面积 = 直角三角形的面积 = $\frac{1}{2}\times 底边\times 高 = \frac{1}{2}\times BC\times OA$

区域 I 的面积 = $\frac{1}{2}\times 32\times 16=256\ cm^2$

同样，区域 II 的面积 $=256\ cm^2$

对于区域 III，

现在，在 $\vartriangle DEF$ 中

设三条边长为 $a=6\ cm,\ b=6\ cm$ 和 $c=8\ cm$

三角形半周长，$s=\frac{a+b+c}{2}=\frac{( 6+6+8)}{2}\ cm=10\ cm$

使用海伦公式，

区域 III（三角形）的面积 = $\sqrt{s( s-a)( s-b)( s-c)}$

$=\sqrt{10(10-6)(10-6)(10-8)}$

$=\sqrt{10\times 4\times 4\times 2}$

$=\sqrt{2\times 5\times 4\times 4\times 2}$

$=\sqrt{2\times 2\times 4\times 4\times 5}$

$=2\times 4\sqrt{5}$

$=8\times 2.24=17.92\ cm^2$

因此，制作风筝时使用颜色 I 的纸张面积为 $256\ cm^2$

制作风筝时使用颜色 II 的纸张面积为 $256\ cm^2$

制作风筝时使用颜色 III 的纸张面积为 $17.92\ cm^2$。

Tutorialspoint

更新于：2022年10月10日

28 次浏览

开启你的 职业生涯

通过完成课程获得认证

开始学习