一个四边形公园ABCD，其中∠C = 90^o。AB = 9 米，BC = 12 米，CD = 5 米，AD = 8 米。
它占地多少面积？

已知：一个四边形公园ABCD，其中$\angle C\ =\ 90^{o} ,\ AB\ =\ 9\ m,\ BC\ =\ 12\ m,\ CD\ =\ 5\ m\ and\ AD\ =\ 8\ m$。

求解：我们需要求出四边形ABCD所占的面积。

解答

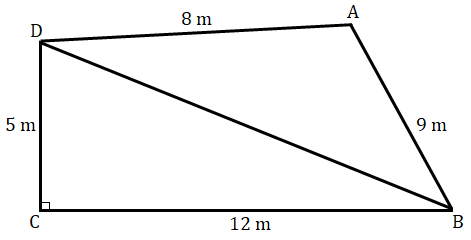
上图显示了四边形公园ABCD。 

ABCD的面积  $=$  $\vartriangle$BCD的面积  $+$  $\vartriangle$ABD的面积

$\vartriangle$BCD是一个直角三角形，因此我们可以很容易地计算出它的面积，但是要计算$\vartriangle$ABD的面积，我们需要边BD的长度，而它的长度也可以通过$\vartriangle$BCD计算出来。

计算边BD的长度:

在直角$\vartriangle$BCD中使用勾股定理；

$BD^2\ =\ BC^2\ +\ DC^2$  

$BD^2\ =\ 12^2\ +\ 5^2$  

$BD^2\ =\ 144\ +\ 25$  

$BD^2\ =\ 169$  

$BD\ =\ \sqrt{169}$  

$\mathbf{BD\ =\ 13\ m}$ 

现在，

$三角形BCD的面积\ =\ \frac{1}{2} \ \times \ 底\ \times \ 高$

$三角形BCD的面积\ =\ \frac{1}{2} \ \times \ 12\ \times \ 5$

$三角形BCD的面积\ =\ 6\ \times \ 5\ =\ 30\ m^{2}$

使用海伦公式计算三角形ABD的面积：  

将三角形ABD的边视为$a\ =\ 9\ m,\ b\ =\ 13\ m\ and\ c\ =\ 8\ m$。所以，

$半周长\ =\ \frac{a\ +\ b\ +\ c}{2}$

$半周长\ =\ \frac{9\ +\ 13\ +\ 8}{2} \ =\ 15\ m$

因此，半周长$=\ 15\ m$。

应用海伦公式:

$三角形ABD的面积\ =\ \sqrt{s( s-a)( s-b)( s-c)}$

$三角形ABD的面积\ =\ \sqrt{15( 15-9)( 15-13)( 15-8)}$

$三角形ABD的面积\ =\ \sqrt{15(6)(2)( 7)}$

$三角形ABD的面积\ =\ \sqrt{1260} \ =\ 35.5\ m^{2}$

因此，

ABCD的面积 $=$ $\vartriangle$BCD的面积 $+$ $\vartriangle$ABD的面积

ABCD的面积 $=\ 30\ +\ 35.50\ m^2$   

ABCD的面积 $=\ \mathbf{65.50\  m^2}$   

所以，四边形ABCD所占的面积是65.50 m$^2$。

Tutorialspoint

更新于： 2022年10月10日

51 次浏览

开启你的 职业生涯

完成课程获得认证

开始学习