三角形$\mathrm{ABC}$ 的角$\mathrm{A}, \mathrm{B}$ 和$\mathrm{C}$ 的角平分线分别交其外接圆于$\mathrm{D}, \mathrm{E}$ 和 $\mathrm{F}$。证明三角形$\mathrm{DEF}$ 的角分别为$90^{\circ}-\frac{1}{2} \mathrm{~A}, 90^{\circ}-\frac{1}{2} \mathrm{~B}$ 和$90^{\circ}-\frac{1}{2} \mathrm{C}$。

已知

三角形$\mathrm{ABC}$ 的角$\mathrm{A}, \mathrm{B}$ 和$\mathrm{C}$ 的角平分线分别交其外接圆于$\mathrm{D}, \mathrm{E}$ 和 $F$。

要求

我们需要证明三角形$\mathrm{DEF}$ 的角分别为$90^{\circ}-\frac{1}{2} \mathrm{~A}, 90^{\circ}-\frac{1}{2} \mathrm{~B}$ 和$90^{\circ}-\frac{1}{2} \mathrm{C}$。

解答

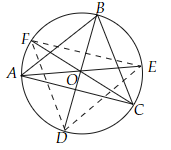
$\angle EDF = \angle EDA + \angle ADF$

$\angle EDA$ 和 $\angle EBA$ 是圆中同一条弦所对的圆周角。

这意味着，

$\angle EDA = \angle EBA$

类似地，

$\angle ADF$ 和 $\angle FCA$ 是圆中同一条弦所对的圆周角。

这意味着，

$\angle A D F=\angle F C A$

$\angle E D F= \angle EDA + \angle ADF$

$=\angle EBA+\angle F C A$

$=\frac{1}{2} \angle B+\frac{1}{2} \angle C$

$\angle D=\frac{\angle B+\angle C}{2}$

$=\frac{180^{\circ}-\angle A}{2}$          (因为 $\angle A+\angle B+\angle C=180^{\circ}$)

$=90^o-\frac{\angle A}{2}$

类似地，

$\angle E=\frac{\angle C+\angle A}{2}$

$\angle E=\frac{180^{\circ}-\angle B}{2}$          (因为 $\angle A+\angle B+\angle C=180^{\circ}$)

$=90^o-\frac{\angle B}{2}$

$\angle E=\frac{\angle A+\angle B}{2}$

$\angle F=\frac{180^{\circ}-\angle C}{2}$            (因为 $\angle A+\angle B+\angle C=180^{\circ}$)

$\angle F=90^{\circ}-\frac{\angle C}{2}$

证毕。

教程点

更新于: 2022年10月10日

45 次查看

开启你的 职业生涯

通过完成课程获得认证

开始学习