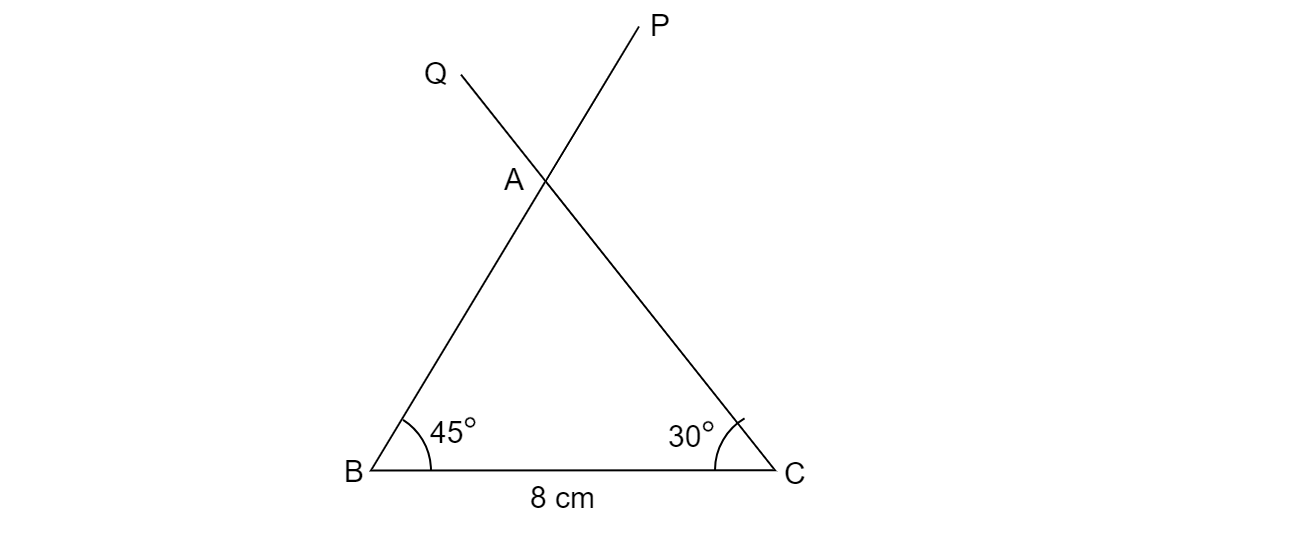
作一个三角形ABC，其中BC$\displaystyle =8$ cm，$\displaystyle \angle $B$\displaystyle =45^{o}$，$\displaystyle \angle $C$\displaystyle =30^{o}$。再作一个与$\displaystyle \vartriangle $ABC相似的三角形，使其各边是$\displaystyle \vartriangle $ABC对应边的$\frac{3}{4} $。
已知：边$BC=8$ cm，$\angle B=45^{o}$， $\angle C=30^{o}$
要求：作$\vartriangle ABC$。并作另一个与$\vartriangle ABC$相似的三角形，使其各边是$\vartriangle ABC$对应边的$\frac{3}{4}$。
解答
按照以下步骤操作
1.画一条线段$\displaystyle BC=8cm$。
2.画$\displaystyle \angle PBC=45^{o} $ 。
3.画$\angle QCB=30^{o}$。
4.直线PB和QC相交于点A。
$\vartriangle ABC$作图完成。
现在我们将作另一个与$\vartriangle ABC$相似的三角形，且其每条边都是$\vartriangle ABC$对应边的$\frac{3}{4}$。
按照以下步骤操作
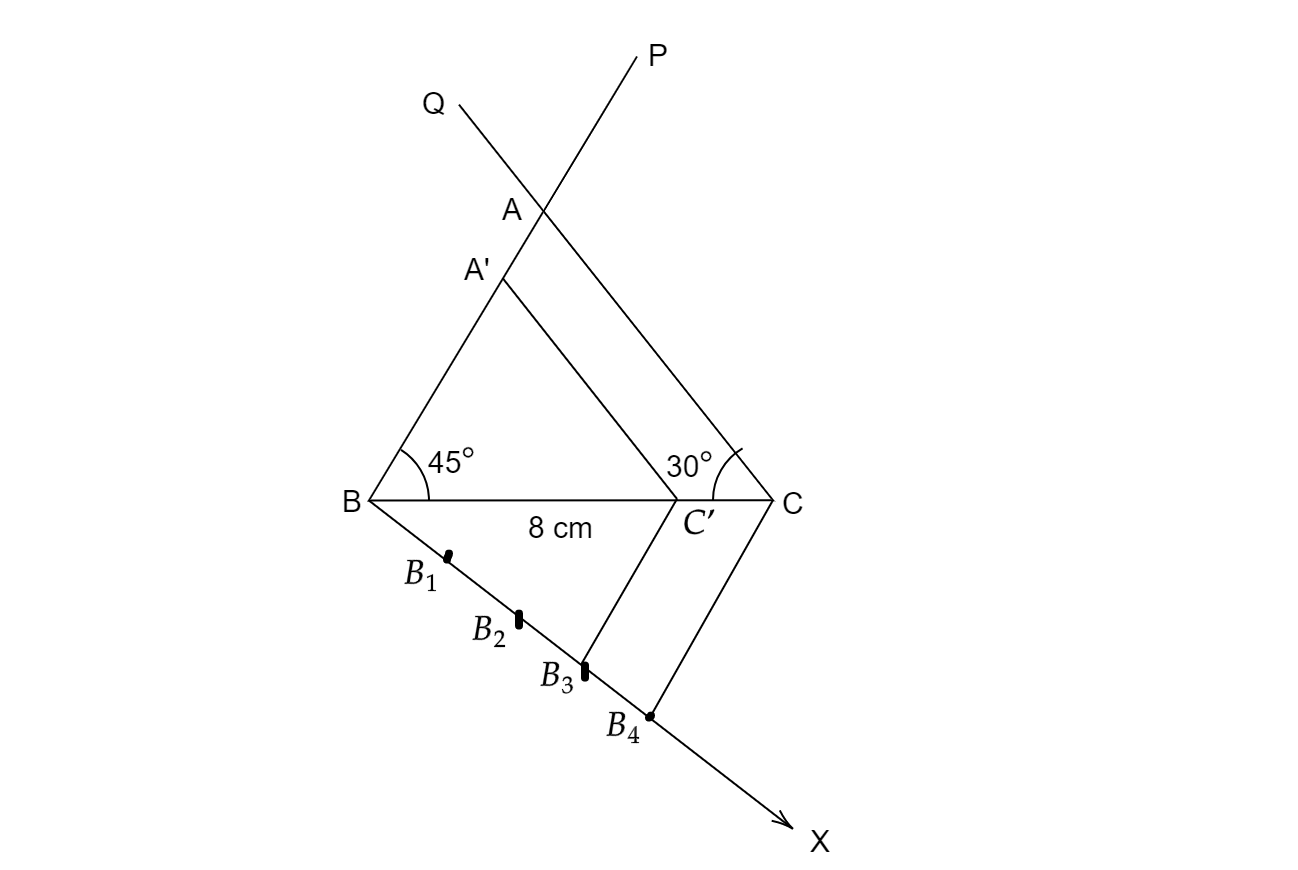
1.画一条射线BX，与顶点A相对，与BC成锐角。
2.将射线BX分成四等份$BB_{1} ,\ B_{1} B_{2} ,\ B_{2} B_{3} ,\ B_{3} B_{4}$。
3.从$B_{4}$到$C$画一条直线。
4.从点$B_{3}$画一条平行于$B_{4} C$的直线，其在$BC$上的端点为$C'$。
5.从点$C'$画一条平行于$AC$的直线，其在直线$AB$上的端点为$\\ A'$.
$\vartriangle A'BC'$与$\vartriangle ABC$相似。且其每条边都是$\vartriangle ABC$的$\frac{3}{4}$。
- 相关文章
- 作一个三角形ABC，其中边$BC=7\ cm$，$\angle B = 45^{o}$，$\angle A = 105^{o}$。然后作另一个三角形，使其各边是ABC对应边的$\frac{3}{4}$倍。
- 作一个$\vartriangle ABC$，其中$AB\ =\ 6\ cm$，$\angle A\ =\ 30^{o}$和$\angle B\ =\ 60^{o}$，作另一个与$\vartriangle ABC$相似的三角形$\vartriangle AB’C’$，其底边$ AB’\ =\ 8\ cm$。
- 点P将连接点$\displaystyle A( 2,1)$和$\displaystyle B( 5,-8)$的线段分成两部分，使得$\displaystyle \frac{AP}{AB} =\frac{1}{3}$。如果P在直线$\displaystyle 2x-y+k=0$上，求k的值。
- 一块三角形土地的尺寸为$\displaystyle\frac{3}{4}$米、$\displaystyle\frac{1}{4}$米和$\displaystyle\frac{1}{2}$米。求这块三角形土地的周长。
- 作一个$\vartriangle ABC$，其中$CA= 6\ cm$，$AB= 5\ cm$和$\angle BAC= 45^{o}$，然后作一个三角形，使其各边是ABC对应边的$\frac {3}{5}$倍。
- 画一个三角形ABC，其中$BC = 6\ cm, AB = 5\ cm$和$\vartriangle ABC=60^{o}$。然后作一个三角形，使其各边是ABC对应边的$\frac{3}{4}$倍。
- 一张矩形纸的长度为 $\displaystyle 12\frac{1}{2} \ cm\ $，宽度为$\displaystyle 10\frac{2}{3} \ cm\ $。求它的周长。
- 画一个三角形ABC，其中边$BC = 7\ cm, ∠B = 45^o, ∠A = 105^o$。然后，作一个三角形，使其各边是$∆ABC$对应边的$\frac{4}{3}$倍。
- 根据角的类型画出下列角：$\displaystyle \begin{array}{{>{\displaystyle}l}} a) \ \angle LMN\ 优角。\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ b) \ \angle y\ \ 钝角\ c) \ \ \angle XYZ\ 周角\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ d) \ \angle 3\ 优角\end{array}$
- 作一个$\triangle ABC$，其中$AB = 5\ cm, \angle B = 60^o$，高$CD = 3\ cm$。作一个与$\triangle ABC$相似的三角形$\triangle AQR$，使得$\triangle AQR$的边长是$\triangle ACB$对应边长的1.5倍。
- 画一个三角形ABC，其中边$BC = 6\ cm, AB = 5\ cm$和$∠ABC = 60^o$。然后作一个三角形，使其各边是三角形$ABC$对应边的$\frac{3}{4}$倍。
- $\displaystyle 如果\ \triangle PQR\ \cong \ \triangle EFD,\ 那么\ \angle E\ =\ ?$a) $\angle P$b) $\angle Q$c) $\angle R$d) 以上都不是
- $\displaystyle 求\ \left[( -2)^{-2}\right]^{-4}的值。$
- 作$\vartriangle ABC$，其中$BC=7\ cm,\ \angle B=75^{o}$和$AB+AC=12\ cm$。
- 作一个$\triangle ABC$，其中$BC = 3.4\ cm, AB - AC = 1.5\ cm$和$\angle B = 45^o$。
数据结构
网络
关系型数据库管理系统
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C语言编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理
化学
生物
数学
英语
经济学
心理学
社会学
时尚研究
法律研究
