根据第 13.5 节给出的符号，推导出圆台的侧面积和全面积公式。

待办事项

我们必须推导出圆锥的圆台的侧面积和全面积公式。

解答

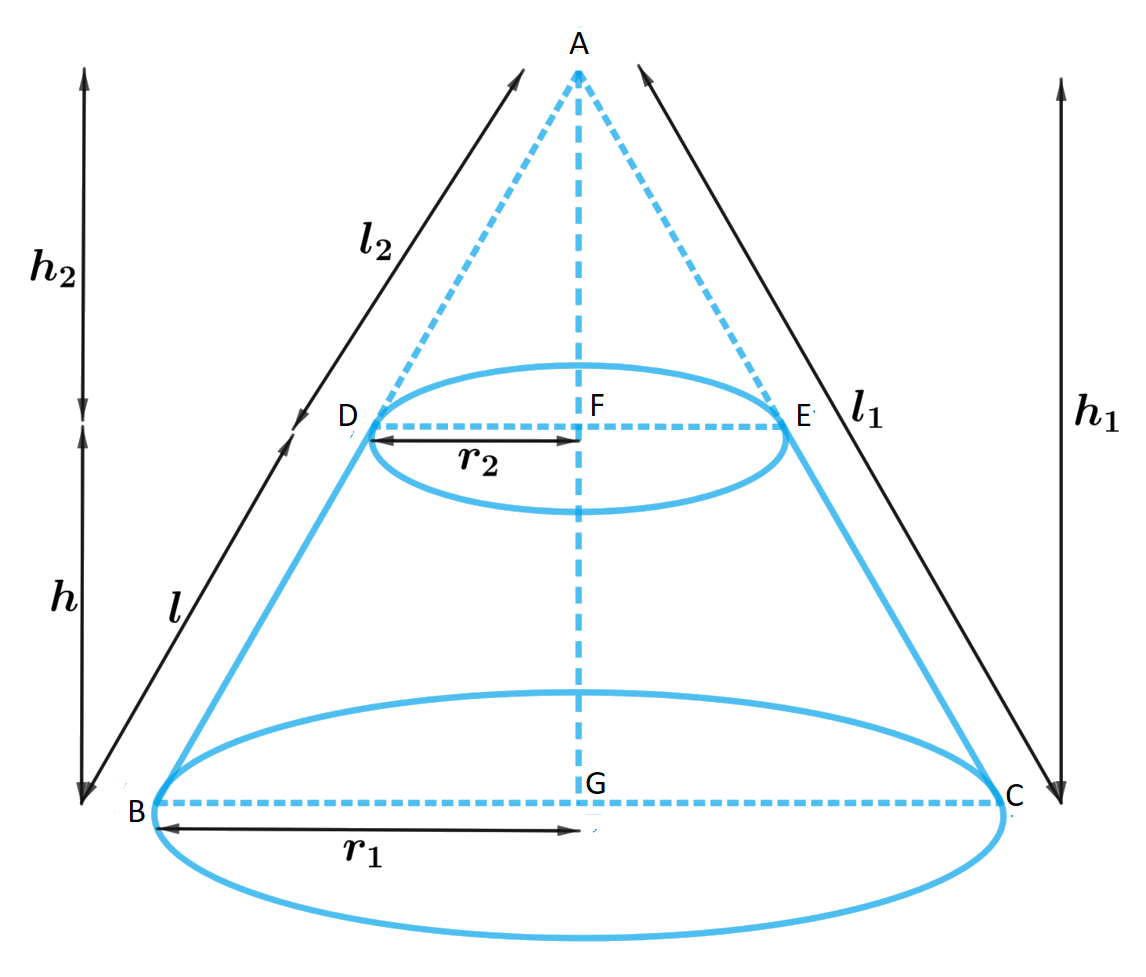
设 ABC 为一个圆锥。

从圆锥中，用平行于底面的平面截出一个圆台 DECB。

设 $r_1$ 和 $r_2$ 为圆台两端的半径，$h$ 为圆台的高。

在 $\triangle ABG$ 和 $\triangle ADF$ 中

$DF \| BG$

因此，

$\triangle ABG \sim \triangle ADF$

这意味着，

$\frac{D F}{B G}=\frac{A F}{A G}=\frac{A D}{A B}$

$\frac{r_{2}}{r_{1}}=\frac{h_{1}-h}{h_{1}}=\frac{l_{1}-l}{l_{1}}$

$\frac{r_{2}}{r_{1}}=1-\frac{h}{h_{1}}=1-\frac{l}{l_{1}}$

$1-\frac{l}{\mathrm{l}_{1}}=\frac{r_{2}}{r_{1}}$

$\frac{l}{l_{1}}=1-\frac{r_{2}}{r_{1}}$

$\frac{l}{l_{1}}=\frac{r_{1}-r_{2}}{r_{1}}$

$\Rightarrow l_{1}=\frac{r_{1} l}{r_{1}-r_{2}}$..............(i)

圆台 DECB 的侧面积 = 圆锥 ABC 的侧面积 - 圆锥 ADE 的侧面积

$=\pi r_{1} l_{1}-\pi r_2(l_{1}-l)$

$=\pi r_{1}(\frac{r_{1}l}{r_{1}-r_{2}})-\pi r_{2}[\frac{r_{1}l}{r_{1}-r_{2}}-l]$

$=\frac{\pi r_{1}^{2} l}{r_{1}-r_{2}}-\pi r_{2}(\frac{r_{1}l-r_{1} l+r_{2}l}{r_{1}-r_{2}})$

$=\frac{\pi r_{1}^{2} l}{r_{1}-r_{2}}-\frac{\pi r_{2}^{2}l}{r_{1}-r_{2}}$

$=\pi l[\frac{r_{1}^{2}-r_{2}^{2}}{r_{1}-r_{2}}]$

$=\pi l[\frac{(r_1-r_2)(r_1+r_2)}{r_1-r_2}]$

$=\pi (r_1+r_2)l$

圆台的全面积 = 圆台 DECB 的侧面积 + 上圆的面积 + 下圆的面积

$=\pi (r_1+r_2)l+\pi r_1^2+\pi r_2^2$

Tutorialspoint

更新于: 2022年10月10日

66 次浏览

开启你的职业生涯

完成课程获得认证

开始学习