绘制多项式 $\mathrm{f}(\mathrm{x})=\mathrm{x}^{2}-2 \mathrm{x}-8$ 的图像。

已知

给定的多项式为 $\mathrm{f}(\mathrm{x})=\mathrm{x}^{2}-2 \mathrm{x}-8$ 。
要求

我们需要绘制给定多项式的图像。

解答

令 $y =f(x)= x^2 - 2x - 8$ 。

下表给出了不同 x 值对应的 $f(x)$ 值。

$x$	$-4$	$-3$	$-2$	$-1$	$0$	$1$	$2$	$3$	$4$	$5$
$f(x)$	16	7	0	$-5$	$-8$	$-9$	$-8$	$-5$	0	7

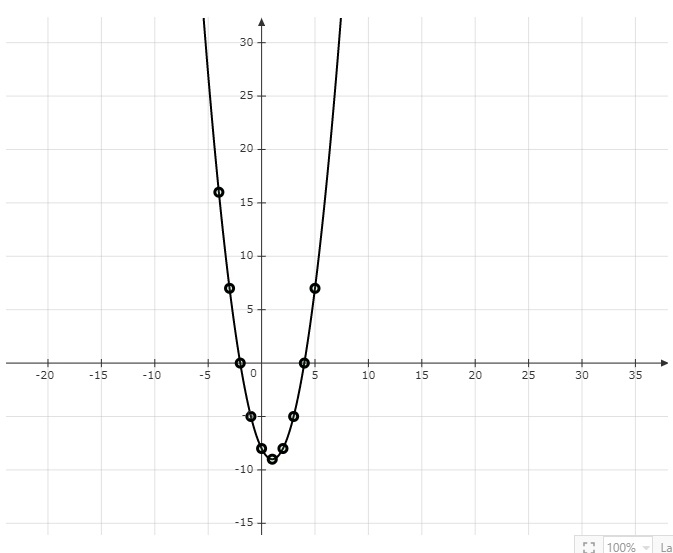
在坐标纸上描点 $(-4, 16), (-3, 7), (-2, 0), (-1, -5), (0, - 8), (1, - 9), (2, - 8), (3, - 5), (4, 0), (5, 7)$ ，并绘制一条经过这些点的曲线。

得到的曲线表示多项式 $f(x) = x^2 - 2x - 8$ 的图像。

教程点

更新于: 2022年10月10日

33 次浏览

完成课程获得认证

绘制多项式f(x)=x2−2x−8 \mathrm{f}(\mathrm{x})=\mathrm{x}^{2}-2 \mathrm{x}-8 的图像。