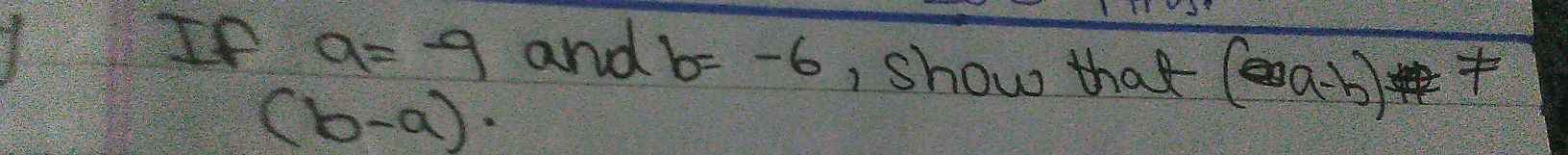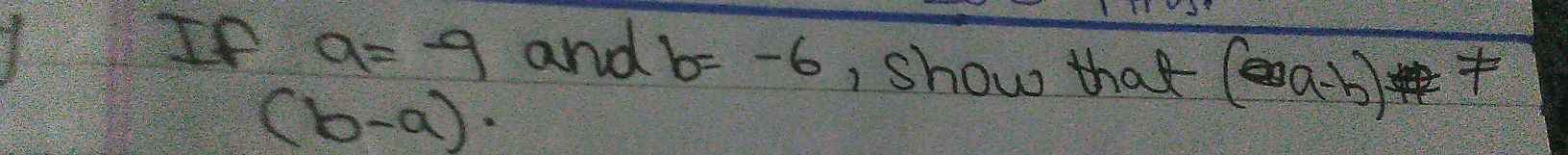如果 a = -9 且 b = -6，证明 (eaa-b)? eq
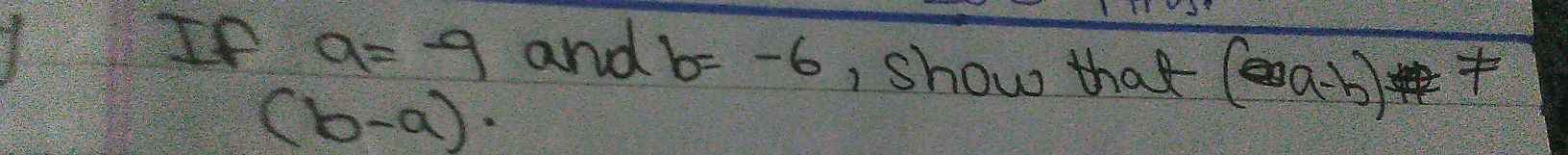
已知
a = -9 且 b = -6
求证：我们需要证明 a - b ≠ b - a
解答：
现在，
(a - b) ≠ (b - a)
((-9) - (-6)) ≠ ((-6) - (-9))
(- 9 + 6) ≠ (- 6 + 9)
(- 3) ≠ (3)
因此得证
- 相关文章
- 如果 $2^{a}=3^{b}=6^{c}$，则证明 $ c=\frac{a b}{a+b} $
- 如果 $\angle A$ 和 $\angle B$ 是锐角，且 $cos\ A = cos\ B$，则证明 $∠A = ∠B$。
- 如果 \( \angle A \) 和 \( \angle B \) 是锐角，且 \( \cos A=\cos B \)，则证明 \( \angle A=\angle B \)。
- 如果 \(n(A)=30, n(B) = 45, n(A \cup B) = 65\) 则求 \(n(A \cap B)\)、\(n(A-B)\) 和 \(n(B-A)\)。
- 如果 \( a+2 b=5; \) 则证明：\( a^{3}+8 b^{3}+30 a b=125 \)。
- 证明 $(a – b)^2, (a^2 + b^2)$ 和 $(a + b)^2$ 成等差数列。
- 由点 $A (9,\ 0),\ B (9,\ 6),\ C (–9,\ 6)$ 和 $D(–9,\ 0)$ 所形成的图形是什么？
- 如果 $a+b = 6$ 且 $ab = 8$，求 $a^2+b^2$。
- 解：\( \frac{\sqrt{x+a}+\sqrt{x-b}}{\sqrt{x+a}-\sqrt{x-b}}=\frac{a+b}{a-b}(a \eq b) \)
- 如果 \( a \) 和 \( b \) 是不同的正素数，使得 \( \sqrt[3]{a^{6} b^{-4}}=a^{x} b^{2 y} \)，求 \( x \) 和 \( y \)。
- 如果 \( a \cos \theta+b \sin \theta=m \) 和 \( a \sin \theta-b \cos \theta=n \)，证明 \( a^{2}+b^{2}=m^{2}+n^{2} \)
- 证明点 $A( 4,\ 2),\ B( 7,\ 5),\ C( 9,\ 7)$ 共线。
- 证明 $(a−b)^2,\ (a^2+b^2),\ (a+b)^2$ 成等差数列。
- 证明 \( \frac{a \sqrt{b}-b \sqrt{a}}{a \sqrt{b}+b \sqrt{a}}=\frac{1}{a-b}(a+b-2 \sqrt{a b}) \)
- 设 $a$ 和 $b$ 为正整数。证明 $\sqrt{2}$ 始终介于 $\frac{2}{b}$ 和 $\frac{a+2 b}{a+b}$ 之间。
数据结构
网络
关系型数据库管理系统
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 语言编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理
化学
生物
数学
英语
经济学
心理学
社会学
时尚研究
法律研究