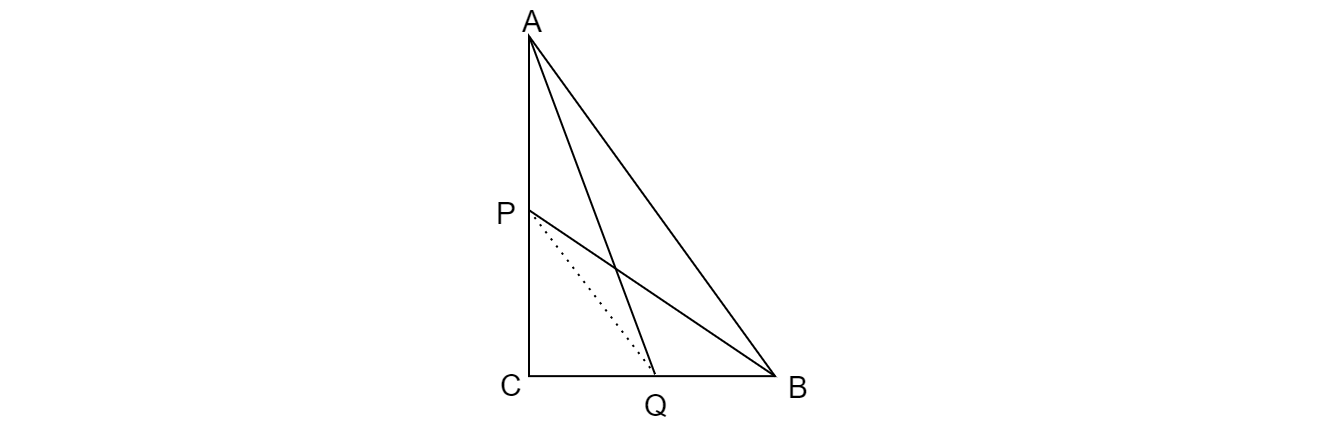
如果$P$和$Q$分别是直角三角形$\vartriangle ABC$（∠C为直角）的边$CA$和$CB$上的点，证明$( AQ^{2}+BP^{2})=( AB^{2}+ PQ^{2})$。

已知：$P$和$Q$分别是直角三角形$\vartriangle ABC$（∠C为直角）的边$CA$和$CB$上的点。

要求：证明$( AQ^{2}+BP^{2})=(AB^{2}+ PQ^{2})$

解答
在$\vartriangle ABC$、$\vartriangle ACQ$、$\vartriangle BPC$、$\vartriangle PCQ$中使用勾股定理，

我们得到

$AB^{2}=AC^{2}+BC^{2}$             ....................$( i)$

$AQ^{2}=AC^{2}+CQ^{2} $          ....................$( ii)$

$BP^{2}=PC^{2}+BC^{2}  $           ................... $( iii)$

$PQ^{2}=PC^{2}+CO^{2} $           ....................$( iv)$

将方程$( ii)$和$( iii)$相加，我们得到

$AQ^{2}+BP^{2}=AC^{2}+CQ^{2}+PC^{2}+BC^{2}$   

$=( AC^{2}+BC^{2})+( CQ^{2}+PC^{2})$

$=AB^{2}+PQ^{2}$

因为$L.H.S=AQ^{2}+BP^{2}$

$=AB^{2}+PQ^{2}=R.H.S$

因此得证。
 

更新于： 2022年10月10日

44 次浏览

开启你的职业生涯

完成课程获得认证

开始学习
广告

© . All rights reserved.