如果从水面以上 $h$ 米处的一点观察云的仰角为 $\alpha$，并且观察到它在湖中的倒影的俯角为 $\beta$，证明云到观察点的距离为 $\frac{2 h \sec \alpha}{\tan \beta-\tan \alpha}$。

已知

从水面以上 $h$ 米处的一点观察云的仰角为 $\alpha$，并且观察到它在湖中的倒影的俯角为 $\beta$。

要求

我们必须证明云到观察点的距离为 $\frac{2 h \tan \alpha}{\tan \beta-\tan \alpha}$。

解答

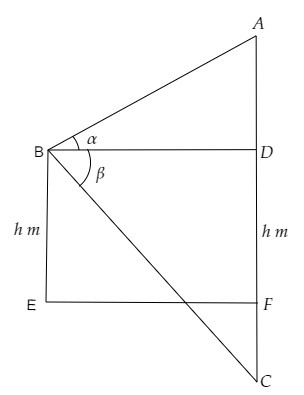
设云为 $A$，湖中的倒影为 $C$，观察点为 $B$。

设 $AD=y\ m$，$FC=h+y\ m$ 以及 $BD=EF=x\ m$。

从图中，

$\angle ABD =\alpha, BE=DF=h\ m$ 以及 $\angle DBC=\beta$

在 $\vartriangle ABD$ 中，

$tan\ \alpha =\frac{AD}{BD} =\frac{y}{x}$

$x=\frac{y}{\tan\ \alpha}$.........(i)

在 $\vartriangle BDC$ 中，

$tan\ \beta=\frac{DC}{BD} =\frac{y+h+h}{x}$

$x=\frac{2h+y}{\tan \beta}$.........(ii)

从 (i) 和 (ii) 中，我们得到，

$\frac{y}{\tan\ \alpha}=\frac{y+2h}{\tan \beta}$

$y\tan \beta=(y+2h)\tan \alpha$

$y(\tan \beta-\tan \alpha)=2h\tan \alpha$

$y=\frac{2h\tan \alpha}{\tan \beta-\tan \alpha}$..............(iii)

在 $\vartriangle ABD$ 中，

$sin\ \alpha =\frac{AD}{AB} =\frac{y}{AB}$

$AB=\frac{\frac{2h\tan \alpha}{\tan \beta-\tan \alpha}}{\sin \alpha}$

$=\frac{\frac{2h(\frac{\sin \alpha}{\cos \alpha})}{\tan \beta-\tan \alpha}}{\sin \alpha}$

$=\frac{2h\sec \alpha}{\tan \beta-\tan \alpha}$

证毕。

教程点

更新于: 2022-10-10

141 次浏览

开启你的 职业生涯

通过完成课程获得认证

开始学习