Loading [MathJax]/jax/output/HTML-CSS/jax.js

一栋房子的窗户距离地面 $h$ 米。从窗户处，观察到另一栋位于巷子对面房屋的顶部和底部的仰角和俯角分别为 $\alpha$ 和 $\beta$ 。证明这栋房屋的高度为 $h( 1+tan\alpha cot\beta)$ 米。

学术数学 NCERT 10 年级

已知：一栋房子的窗户距离地面

$h$ 米。从窗户处，观察到另一栋位于巷子对面房屋的顶部和底部的仰角和俯角分别为

$\alpha$ 和

$\beta$ 。

要求：证明这栋房屋的高度为

$h( 1+tan\alpha cot\beta)$ 米。

解答

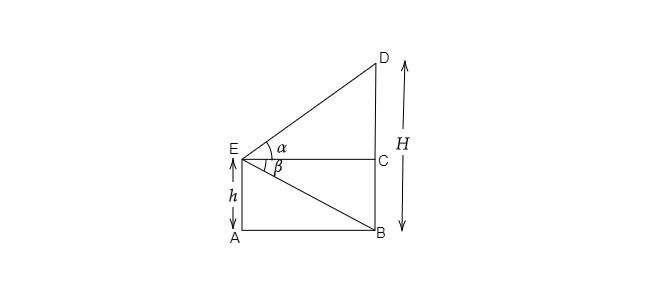
设另一栋房屋的高度为 '

$H$ '。

现在，在

$\vartriangle DEC$ 中，

$\Rightarrow tan\alpha =\frac{DC}{EC}$

$=\frac{H-h}{EC}$

$\Rightarrow EC=\frac{H-h}{tan\alpha}\ .....\ ( i)$

在

$\vartriangle EBA$ 中，

$\Rightarrow tan\beta =\frac{EA}{AB}$

$=\frac{h}{EC}\ .......\ [\therefore AB=EC]$

$\Rightarrow EC=\frac{h}{tan\beta }\ ....... ( ii)$

由

$( i)$ 和

$( ii)$ ，得到

$\Rightarrow \frac{h}{tan\beta}=\frac{H−h}{tan\alpha}$

$\Rightarrow htan\alpha =Htan\beta −htan\beta$

$\Rightarrow H tan\beta =h(tan\alpha +tan\beta )$

$\Rightarrow H=h( \frac{tan\alpha}{tan\beta}+\frac{tan\beta}{tan\beta})$

$\Rightarrow H=h(1+tan\alpha cot\beta )$

因此，得证。

教程点

更新于： 2022年10月10日

88 次浏览

开启你的职业生涯

通过完成课程获得认证

广告