数据结构
网络
关系数据库管理系统 (RDBMS)
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C语言编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理学
化学
生物学
数学
英语
经济学
心理学
社会学
服装设计
法学一栋房子的下窗户距离地面 2 米高，上窗户垂直距离下窗户 4 米。某一时刻，从这两个窗户观察到一个气球的仰角分别为 60° 和 30°。求气球距离地面的高度。
已知
一栋房子的下窗户距离地面 2 米高，上窗户垂直距离下窗户 4 米。
某一时刻，从这两个窗户观察到一个气球的仰角分别为 60° 和 30°。
要求
我们必须找到气球距离地面的高度。
解答
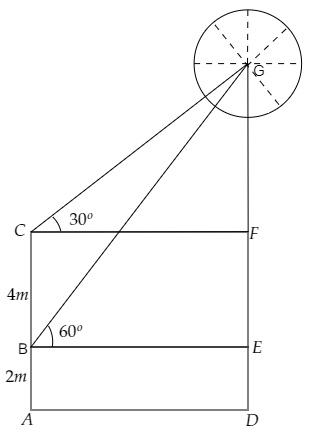
设气球距离地面的高度为 H 米。
从图中可以看出，
AB = ED = 2 米
BC = EF = 4 米
GF = DG – (FE + ED)
= H – (4 + 2)
= H – 6 米
∠GCF = 30°
∠GBE = 60°
设 AD = BE = CF = x 米
在△GBE中，
tan 60° = GE / BE
√3 = (H - 6 + 4) / x
⇒ x = (H - 2) / √3 ……(i)
在△GCF中，
tan 30° = GF / CF
tan 30° = (H - 6) / x = 1 / √3
⇒ x = √3(H - 6) ……(ii)
由公式 (i) 和 (ii)，
√3(H - 6) = (H - 2) / √3
3(H - 6) = H - 2
⇒ 3H - 18 = H - 2
⇒ 2H = 16
⇒ H = 8 米
因此，气球距离地面的高度为 8 米。
更新于：2022年10月10日
444 次浏览
广告