一个气球通过一根长为\( 215 \mathrm{~m} \)的缆绳与气象地面站相连，缆绳与水平面成\( 60^{\circ} \)角。确定气球离地面的高度。假设缆绳没有松弛。

已知

一个气球通过一根长为\( 215 \mathrm{~m} \)的缆绳与气象地面站相连，缆绳与水平面成\( 60^{\circ} \)角。

需要完成

我们需要确定气球离地面的高度。

解：  

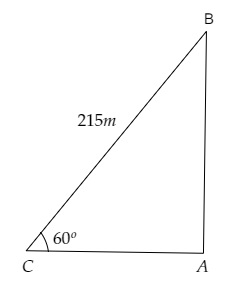
设 $C$ 为气象地面站，$AB$ 为气球离地面的高度。

从图中可以看出，

$\mathrm{BC}=215 \mathrm{~m}, \angle \mathrm{BCA}=60^{\circ}$

设气球离地面的高度为 $\mathrm{AB}=h \mathrm{~m}$。

我们知道，

$\sin \theta=\frac{\text { 对边 }}{\text { 斜边 }}$

$=\frac{\text { AB }}{BC}$

$\Rightarrow \sin 60^{\circ}=\frac{h}{215}$

$\Rightarrow \frac{\sqrt3}{2}=\frac{h}{215}$

$\Rightarrow (215)\frac{\sqrt3}{2}=h \mathrm{~m}$

$\Rightarrow h=\frac{215(1.732)}{2} \mathrm{~m}$

$\Rightarrow h=185.975 \mathrm{~m}$

$\Rightarrow h=186 \mathrm{~m}$

因此，气球离地面的高度为 $186 \mathrm{~m}$。

教程点

更新于： 2022年10月10日

41 次浏览

开启你的 职业生涯

完成课程获得认证

开始学习