一棵垂直生长的树，高$15 \mathrm{~m}$，被风吹断，树顶刚好触地，与地面成$60^{\circ}$角。树断裂处离地面的高度是多少？

已知

一棵垂直生长的树，高$15 \mathrm{~m}$，被风吹断，树顶刚好触地，与地面成$60^{\circ}$角。

解题步骤

我们需要找到树断裂处离地面的高度。

解：  

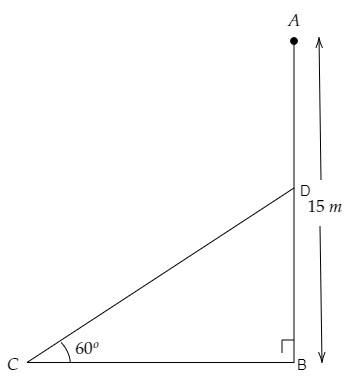
设AB为树的原高度，DB为树断裂处离地面的高度。

设C点为树顶触地处。

由图可知：

$\mathrm{AB}=15 \mathrm{~m}, \angle \mathrm{DCB}=60^{\circ}$

设树断裂处离地面的高度为$\mathrm{DB}=x \mathrm{~m}$，断裂部分的高度为$\mathrm{DC}=15-x \mathrm{~m}$。

我们知道：

$\sin \theta=\frac{\text { 对边 }}{\text { 斜边 }}$

$=\frac{\text { DB }}{DC}$

$\Rightarrow \sin 60^{\circ}=\frac{x}{15-x}$

$\Rightarrow \frac{\sqrt3}{2}=\frac{x}{15-x}$

$\Rightarrow (15-x)\sqrt3=2x$

$\Rightarrow 2x+1.732x=15(1.732)$

$\Rightarrow 3.732x=25.98$

$\Rightarrow x=\frac{25.98}{3.732}$

$\Rightarrow x=6.9$

因此，树断裂处离地面$6.9 \mathrm{~m}$。   

教程点

更新于：2022年10月10日

浏览量：124

开启你的职业生涯

完成课程获得认证

开始学习