从地面上一点观察某垂直塔顶部的仰角为60°。从第一点垂直向上10米处另一点观察塔顶部的仰角为30°。求塔的高度。

已知：从地面和地面以上10米处分别测得的仰角为60°和30°。

求解：求塔的高度。

假设AB为塔，如图所示，∠ACB=60°，∠ADE=30°

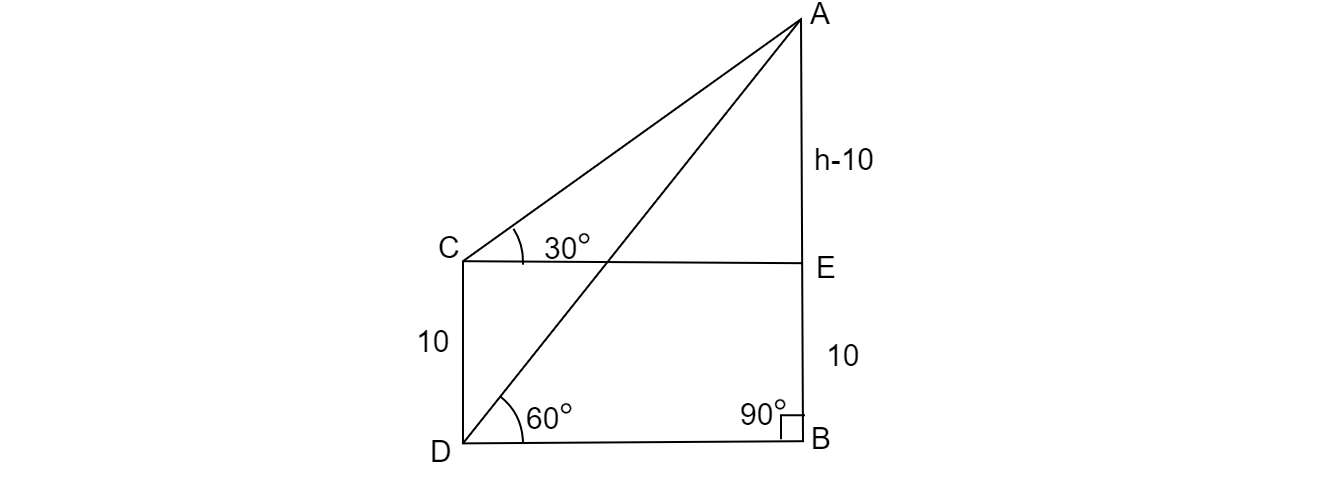
设塔高为h米。

已知CD=BE=10米

在△ABC中，tan60° = AB/BC = h/BC = √3 $( \because \ tan60^{o} =\sqrt{3})$

或 BC = h/√3

在△ADE中，tan30° = AE/DE = (h-10)/BC $\left( \because \ tan30^{o} =\frac{1}{\sqrt{3}}\right) \ $

=(h-10)/(h/√3)

=> √3(h-10)/h = 1/√3

=> 3(h-10) = h

=> 3h - 30 = h

=> 2h = 30

=> h = 15米

∴ 塔高为15米。