一座高 30 米的塔的顶部从另一座在同一平面上的塔的底部仰角为 60°，第二座塔的顶部从第一座塔的底部仰角为 30°。求这两座塔之间的距离。

已知：一座高 30 米的塔的顶部从另一座在同一平面上的塔的底部仰角为 60°，第二座塔的顶部从第一座塔的底部仰角为 30°。

求解：求这两座塔之间的距离。

解

设两塔之间的距离为 AB=x 米，另一座塔的高度为 PA=h 米



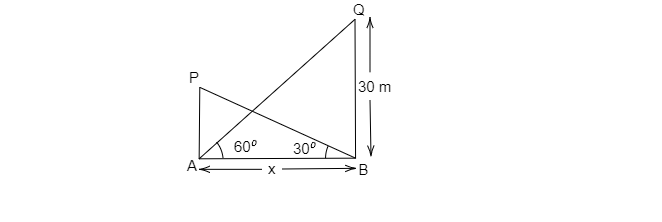
已知塔的高度为 QB=30 米，且∠QAB=60°，∠PBA=30°

现在，在△QAB 中，

tan60°=QB/AB=30/x

⇒√3=30/x

⇒x=30/√3 * √3/√3

⇒x=30√3/3=10√3 米

因此，两塔之间的距离为 10√3 米。

更新于： 2022-10-10

348 次浏览

开启你的职业生涯

通过完成课程获得认证

开始学习
广告