数据结构
网络
关系数据库管理系统(RDBMS)
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C语言编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理
化学
生物
数学
英语
经济学
心理学
社会研究
服装研究
法律研究从一栋\( 15 \mathrm{~m} \) 高的建筑物顶部，测得塔顶的仰角为\( 30^{\circ} \)。从同一栋建筑物的底部，测得塔顶的仰角为\( 60^{\circ} \)。求塔高和塔与建筑物之间的距离。
已知
从一栋\( 15 \mathrm{~m} \) 高的建筑物顶部，测得塔顶的仰角为\( 30^{\circ} \)。
从同一栋建筑物的底部，测得塔顶的仰角为\( 60^{\circ} \)。
要求
我们必须求出塔高和塔与建筑物之间的距离。
解：
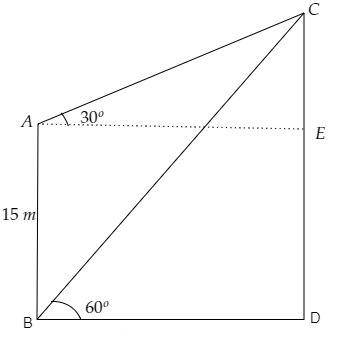
设CD为建筑物，AB为塔。
从图中，
$\mathrm{AB}=15 \mathrm{~m}, \angle \mathrm{CAE}=30^{\circ}, \angle \mathrm{CBD}=60^{\circ}$
设塔高为$\mathrm{CD}=h \mathrm{~m}$，塔与建筑物之间的距离为$\mathrm{BD}=x \mathrm{~m}$。
这意味着，
$\mathrm{AE}=\mathrm{BD}=x \mathrm{~m}$
$\mathrm{ED}=\mathrm{AB}=15 \mathrm{~m}$ and $\mathrm{CE}=h-15 \mathrm{~m}$
我们知道，
$\tan \theta=\frac{\text { 对边 }}{\text { 邻边 }}$
$=\frac{\text { CE }}{AE}$
$\Rightarrow \tan 30^{\circ}=\frac{h-15}{x}$
$\Rightarrow \frac{1}{\sqrt3}=\frac{h-15}{x}$
$\Rightarrow x=(h-15)(\sqrt3) \mathrm{~m}$
$\Rightarrow x=\sqrt3 (h-15) \mathrm{~m}$...........(i)
类似地，
$\tan \theta=\frac{\text { 对边 }}{\text { 邻边 }}$
$=\frac{\text { CD }}{DB}$
$\Rightarrow \tan 60^{\circ}=\frac{h}{x}$
$\Rightarrow \sqrt3=\frac{h}{x}$
$\Rightarrow (x)\sqrt3=h \mathrm{~m}$
$\Rightarrow [\sqrt3 (h-15)]\sqrt3=h \mathrm{~m}$ [从 (i)]
$\Rightarrow 3(h-15)=h \mathrm{~m}$
$\Rightarrow 3h-h=45 \mathrm{~m}$
$\Rightarrow h=\frac{45}{2}=22.5 \mathrm{~m}$
$\Rightarrow x=1.732(22.5-15)=1.732(7.5)=12.975 \mathrm{~m}$
因此，塔高为\(22.5 \mathrm{~m}\)，塔与建筑物之间的距离为\(12.975 \mathrm{~m}\)。
85 次浏览
