从一栋7米高的建筑物顶部，塔顶的仰角为$60^{o}$，塔底的俯角为$30^{o}$。求塔的高度。

已知：建筑物高度$=7$ 米，塔顶的仰角$=60^{o}$，塔底的俯角$=30^{o}$

要求：求塔的高度。

设AB为建筑物，CD为塔

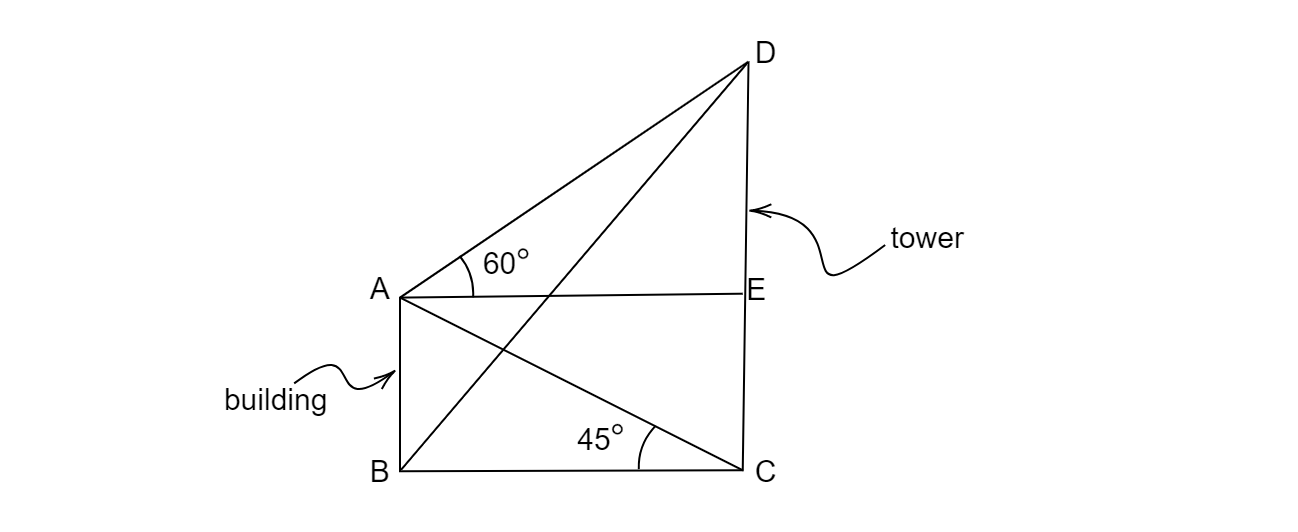
根据题意

$\angle EAD=60^{o}$

$\because AE\parallel BC$

$\Rightarrow \angle ACB=\angle EAC=45^{o}$

在$\vartriangle ABC$中，$tan45^{o} =\frac{AB}{BC} =\frac{7}{BC} =1$          $(   \because tan45^{o} =1)$

$BC=7$

$BC=AE=7$

现在在$\vartriangle AED$中

$tan60^{o} =\sqrt{3} =\frac{DE}{AE} =\frac{DE}{7}$

$\Rightarrow DE=7\sqrt{3}$

我们知道塔的高度为 $CD=CE+ED=7+7\sqrt{3} =7\left( 1+\sqrt{3}\right)$

$=19.13$ 米。