塔顶的仰角是 $30^o$。如果塔的高度加倍，那么检查塔顶的仰角是否也会加倍。

已知：塔顶的仰角为 $30^o$。如果塔的高度加倍。

要求：检查塔顶的仰角。

给定的仰角 $=30^o$。

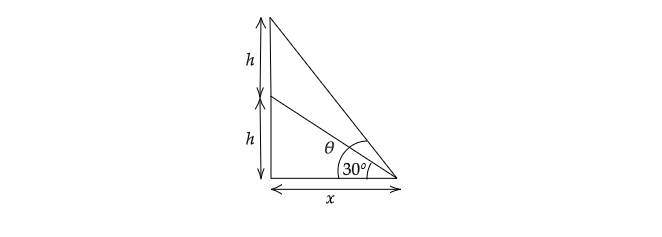
设塔高 $=h$，观察者距离塔底的距离为 $x$。

则：

$\frac{h}{x}=tan30^o=\frac{1}{\sqrt{3}}\ ........\ ( i)$

如果塔的高度加倍，则新的高度 $=2h$。

 

设塔顶的仰角为 $\theta$。

则， $tan\theta =\frac{2h}{x}=2\times \frac{1}{\sqrt{3}}=\frac{2}{\sqrt{3}}\ ........( ii)$

但是如果仰角加倍，则应为 $\theta =2\times 30^o=60^o$。

则， $tan\theta =tan60^o=\sqrt{3}\ ........\ ( iii)$。

比较 $( ii)$ & $( iii)$，存在矛盾。