从地面上一点 X 观察一垂直塔 PQ 的顶端 Q 的仰角为 $60^{o}$ 。从 X 垂直向上 40 米的点 Y，观察塔顶 Q 的仰角为 $45^{o}$ 。求塔 PQ 的高度和距离 PX。 $( 使用\ \sqrt{3} \ =\ 1.73)$

学术数学 NCERT 10 年级

已知：从地面上一点 X 观察一垂直塔 PQ 的顶端 Q 的仰角为

$60^{o}$ 。从 X 垂直向上 40 米的点 Y，观察塔顶 Q 的仰角为

$45^{o}$ 。

求解：求塔 PQ 的高度和距离 PX。

解

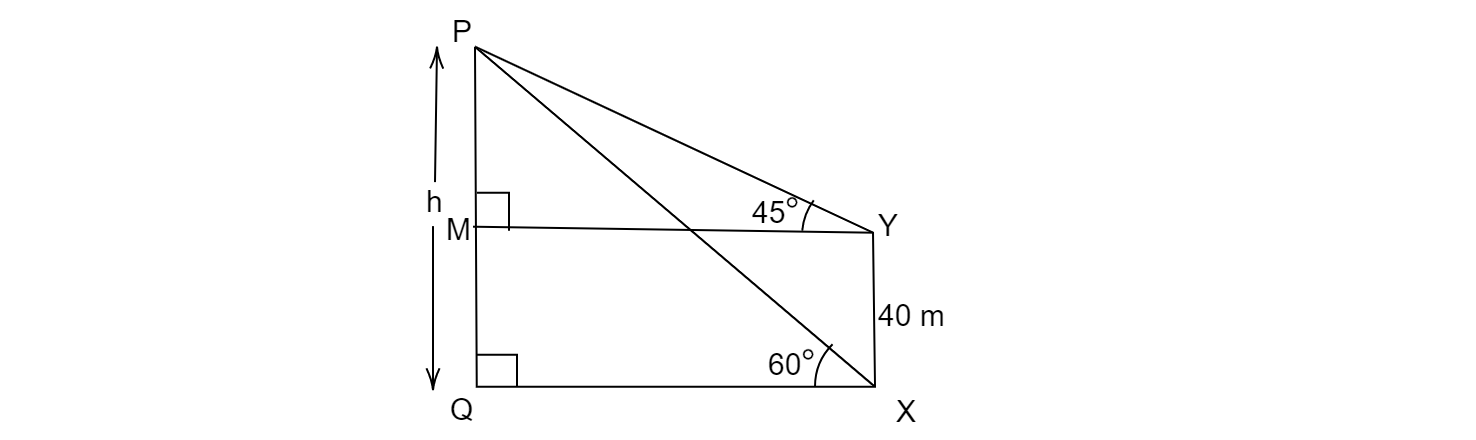
$MP= YX=40\ m$

$\therefore QM = h –40$

在直角三角形

$\vartriangle QMY$ 中，

$tan45^{o} =\frac{QM}{MY} =1=\frac{h-40}{PX} \ \ \ \ \ \ \ \ ( \because \ MY\ =\ PX)$

$\therefore PX = h –40 \ \ \ \ \ \ ....( 1)$

在直角三角形

$\vartriangle QPX$ 中，

$tan\ 60^{o} =\frac{OP}{PX} =\sqrt{3} =\frac{h}{PX} =\frac{h}{h-40} \ \ \ ....( 2)$

$\Rightarrow \frac{h}{h-40} =\sqrt{3}$

$\Rightarrow h=h\sqrt{3} -40\sqrt{3}$

$\Rightarrow h\sqrt{3} -h=40\sqrt{3}$

$\Rightarrow h\times 1.73-h=40\times 1.73$

$\Rightarrow 0.73h=69.2$

或

$h=\frac{69.2}{0.73}$

因此，

$PQ$ 为

$94.79\ m$ 。

教程点

更新于： 2022年10月10日

1K+ 次浏览

开启你的职业生涯

完成课程获得认证

广告