从水面以上 2500 米高处的一点观察到静止的云的仰角为 15°，观察到它在湖中的倒影的俯角为 45°。求云层距离湖面的高度？ (使用 tan 15°=0.268)。

已知

从水面以上 2500 米高处的一点观察到静止的云的仰角为 15°，观察到它在湖中的倒影的俯角为 45°。

要求

我们必须找到云层距离湖面的高度

解答


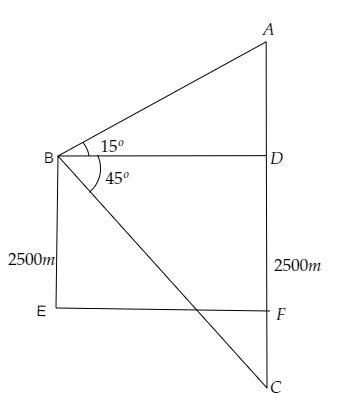
设云为 A，其在湖中的倒影为 C，观察点为 B。

设 AF=FC=h 米，BD=EF=x 米。

从图中，

∠ABD =15°，BE=DF=2500 米，∠DBC=45°

这意味着，

AD=h-2500 米

在△ABD 中，

tan 15° = AD/BD = (h-2500)/x

x=(h-2500)/tan 15°.........(i)

在△BDC 中，

tan 45°=DC/BD = (h+2500)/x

1=(h+2500)/x

x=h+2500 米

将 x=h+2500 代入方程 (i)，得到，

h+2500=(h-2500)/0.268

(h+2500)0.268=h-2500 米

h(1-0.268)=670+2500 米

h=3170/0.732 = 4330 米

因此，云层距离湖面的高度为 4300 米。

更新于： 2022 年 10 月 10 日

44 次浏览

开启你的职业生涯

通过完成课程获得认证

开始学习
广告