数据结构
网络
关系数据库管理系统 (RDBMS)
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C语言编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理学
化学
生物学
数学
英语
经济学
心理学
社会学
时尚研究
法学研究一个人站在船甲板上，甲板距离水面8米。他观察到一座山顶的仰角为60°，山脚的俯角为30°。计算这座山与船的距离以及山的高度。
已知条件
一个人站在船甲板上，甲板距离水面8米。他观察到一座山顶的仰角为60°，山脚的俯角为30°。
解题步骤
我们需要求出这座山与船的距离以及山的高度。
解题过程
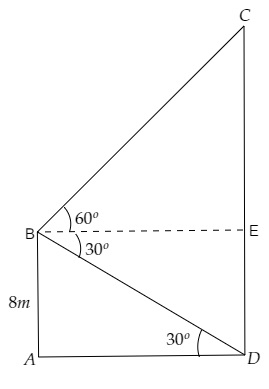
设CD为山，人站在船AB的B点甲板上。
从B点观察到山崖CD底端D点的俯角为30°，从B点观察到山崖CD顶端C点的仰角为60°。
设山崖高度为h米。
根据图示：
∠ADB = 30°，AB = 8米，∠CBE = 60°
这意味着：
ED = AB = 8米，CE = h - 8米
在△CBE中：
tan 60° = CE/BE = (h - 8)/x
√3 = (h - 8)/x
x = (h - 8)/√3 .........(i)
在△ABD中：
tan 30° = AB/AD = 8/x
1/√3 = 8/x
x = 8√3 米 .........(ii)
由(i)和(ii)可得：
(h - 8)/√3 = 8√3
h - 8 = 8√3(√3) 米
h - 8 = 24 米
h = 32 米
因此，山与船的距离为8√3米，山的高度为32米。
更新于：2022年10月10日
浏览量：55
广告