一名站在船甲板上的人，甲板距离水面10米，观察到一座山顶的仰角为60°，山脚的俯角为30°。求这座山与船的距离以及山的高度。

已知：甲板距水面的高度 = 10米，山顶的仰角 = 60°，山脚的俯角 = 30°。

求解：求山与船的距离以及山的高度。

解法

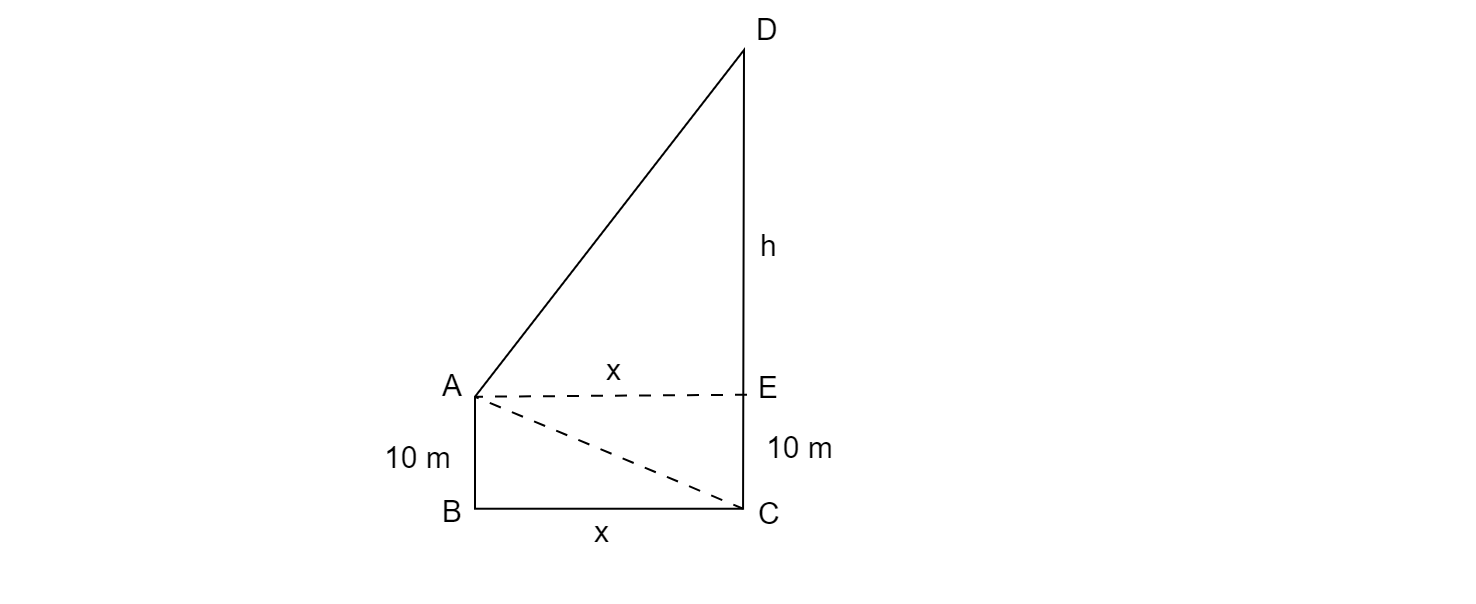
设CD为山，假设该人在船的甲板A点上。

从A点观察到山脚C点的俯角为30°

从A点观察到山顶D点的仰角为60°。

$\therefore \angle EAD =60^{o}$ 且 $\angle BCA=30^{o}$

在$\vartriangle AED$中，

$tan 60^{o} =\frac{DE}{EA} =\frac{h}{x}$

$\sqrt{3} =\frac{h}{x}$

$h=\sqrt{3} x\ \ ...............( 1)$

在$\vartriangle ABC$中，

$tan 30^{o}=\frac{AB}{BC} =\frac{10}{x}$

$\frac{1}{\sqrt{3}} =\frac{10}{x}$

$x=10\sqrt{3} \ m$

代入公式(1)，得 $x=10\sqrt{3}$

$h=10\sqrt{3} \times \sqrt{3}$

$=10 \times 3 = 30\ m$

$DE = 30\ m$

$CD=CE + ED = 10 + 30 = 40\ m$

因此，山与船的距离为$10\sqrt{3} \ m$，山的高度为40米。

 

更新于：2022年10月10日

6K+ 次浏览

开启您的职业生涯

完成课程后获得认证

开始学习
广告