在下列各题中，给出了六个三角比中的一个。求其他三角比的值。$\sin \theta=\frac{\sqrt{3}}{2}$

已知

$\sin \theta=\frac{\sqrt3}{2}$

要求

我们必须找到其他三角比的值。

解：  

我们知道，

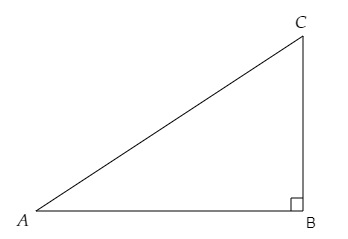
在直角三角形$ABC$中，$\angle B = 90^\circ$，

根据勾股定理，

$AC^2=AB^2+BC^2$

根据三角比的定义，

$sin\ A=\frac{对边}{斜边}=\frac{BC}{AC}$

$cos\ A=\frac{邻边}{斜边}=\frac{AB}{AC}$

$tan\ A=\frac{对边}{邻边}=\frac{BC}{AB}$

$cosec\ A=\frac{斜边}{对边}=\frac{AC}{BC}$

$sec\ A=\frac{斜边}{邻边}=\frac{AC}{AB}$

$cot\ A=\frac{邻边}{对边}=\frac{AB}{BC}$

这里，

设 $sin\ \theta=\frac{BC}{AC}=\frac{\sqrt3}{2}$

$AC^2=AB^2+BC^2$

$\Rightarrow AC^2 = BC^2 + AB^2$ $\Rightarrow 2^2 = (\sqrt{3})^2 + AB^2$

$\Rightarrow AB^2=4-3$

$\Rightarrow AB=\sqrt1=1$

因此，

$cos\ \theta=\frac{AB}{AC}=\frac{1}{2}$

$tan\ \theta=\frac{BC}{AB}=\frac{\sqrt3}{1}=\sqrt3$

$cosec\ \theta=\frac{AC}{BC}=\frac{2}{\sqrt3}$

$sec\ \theta=\frac{AC}{AB}=\frac{2}{1}=2$

$cot\ \theta=\frac{AB}{BC}=\frac{1}{\sqrt3}$ 

教程点

更新于：2022年10月10日

36 次浏览

开启你的职业生涯

完成课程获得认证

开始学习