如图所示，$AB$ 将 $\angle DAC$ 按 $1:3$ 的比例分割，且 $AB = DB$。求 $x$ 的值。

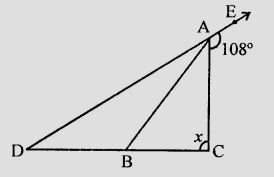
已知

$AB$ 将 $\angle DAC$ 按 $1:3$ 的比例分割，且 $AB = DB$。

要求

求 $x$ 的值。

解答

$\angle CAE + \angle DAC = 180^{\circ}$ (邻补角)

$108^{\circ} + \angle DAC = 180^{\circ}$

$\angle DAC = 180^{\circ} - 108^{\circ}$

$= 72^{\circ}$

$\angle DAB = 72^{\circ} \times \frac{1}{1+3}$

$= \frac{72^{\circ} \times 1}{4}$

$= 18^{\circ}$

$\angle CAB = 72^{\circ} \times \frac{3}{4}$

$= 54^{\circ}$

等边对等角。

这意味着：

$\angle DAB = \angle ADB = 18^{\circ}$ (因为 $AB = DB$)

在 $\triangle ADC$ 中，

$\angle CAE = \angle BDA + \angle ACD$

$108^{\circ} = 18^{\circ} + x$

$x = 108^{\circ} - 18^{\circ}$

$x = 90^{\circ}$

$x$ 的值为 $90^\circ$。

教程点

更新于：2022年10月10日

浏览量：83

开启你的职业生涯

完成课程获得认证

开始学习