数据结构
网络
关系型数据库管理系统
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C语言编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理
化学
生物
数学
英语
经济学
心理学
社会学
服装设计
法律研究在图上表示以下方程组，并写出直线与y轴交点的坐标：$x+3y=6$，$2x-3y=12$
已知
给定的方程组是
$x+3y=6$
$2x-3y=12$
要求：
我们需要在图上表示给定的方程组，并找到直线与y轴交点的坐标。
解答
给定的方程组是
$x+3y-6=0$....(i)
$3y=6-x$
$y=\frac{6-x}{3}$
$2x-3y-12=0$.....(ii)
$3y=2x-12$
$y=\frac{2x-12}{3}$
为了在图上表示上述方程，我们需要至少两个解。
对于方程 (i)，
如果 $x=0$，则 $y=\frac{6-0}{3}=\frac{6}{3}=2$
如果 $x=6$，则 $y=\frac{6-6}{3}=\frac{0}{3}=0$
$x$ | $0$ | $6$ |
$y$ | $2$ | $0$ |
对于方程 (ii)，
如果 $x=0$，则 $y=\frac{2(0)-12}{3}=\frac{-12}{3}=-4$
如果 $x=6$，则 $y=\frac{2(6)-12}{3}=\frac{12-12}{3}=\frac{0}{3}=0$
$x$ | $0$ | $6$ |
| $y$ | $-4$ | $0$ |
上述情况可以在图上表示如下
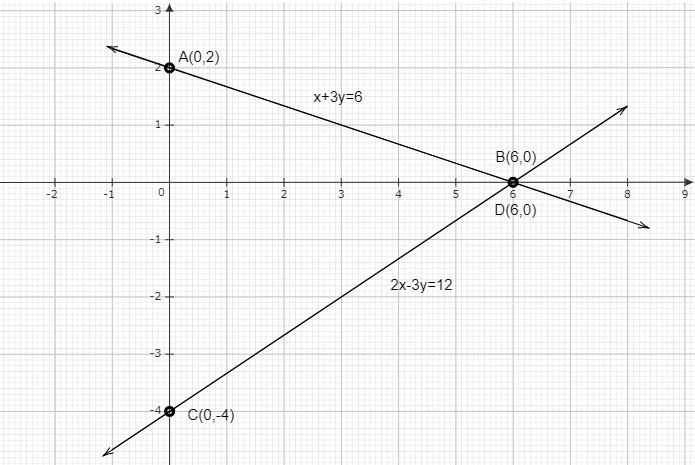
直线 AB 和 CD 分别表示方程 $x+3y=6$ 和 $2x-3y=12$。
给定方程组的解是直线 AB 和 CD 的交点，这些直线分别在点 A 和 C 与 Y 轴相交。
因此，给定方程组的解是 $x=6$ 和 $y=0$。方程 $x+3y=6$ 和 $2x-3y=12$ 所表示的直线分别与 Y 轴交于 $(0,2)$ 和 $(0,-4)$。
更新时间： 2022年10月10日
202 次浏览
广告