以下频数分布给出了某地区 68 位用户的月度用电量。求出数据的平均数、中位数和众数，并进行比较。

月度用电量：（单位）	65-85	85-105	105-125	125-145	145-165	165-185	185-205
用户数	4	5	13	20	14	8	4

已知

给定的频数分布给出了某地区 68 位用户的月度用电量。

要求

我们需要求出数据的平均数、中位数和众数，并进行比较。

解答

给定数据的频数如下所示。

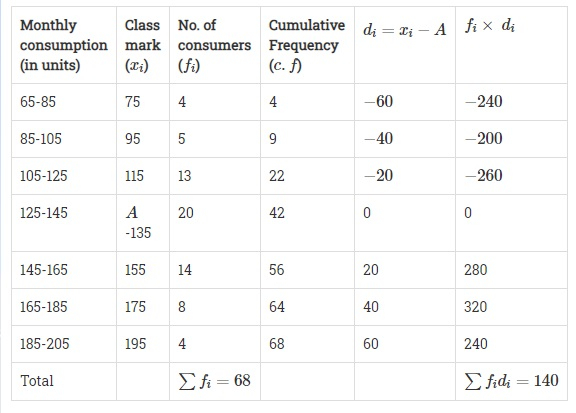
设假定平均数为 $A=135$。

我们知道，

平均数 $=A+\frac{\sum{f_id_i}}{\sum{f_i}}$

因此，

平均数 $=135+\frac{140}{68}$

$=135+2.05$

$=137.05$

给定数据的平均数为 137.05。

我们观察到 125-145 类区间具有最大频数（20）。

因此，它是众数类。

这里，

$l=125, h=20, f=20, f_1=13, f_2=14$

我们知道，

众数 $=l+\frac{f-f_1}{2 f-f_1-f_2} \times h$

$=125+\frac{20-13}{2 \times 20-13-14} \times 20$

$=125+\frac{7}{40-27} \times 20$

$=125+\frac{140}{13}$

$=125+10.76$

$=135.76$

给定数据的众数为 135.76。

这里，

$N=68$

这意味着， $\frac{N}{2}=\frac{68}{2}=34$

中位数类 $=125-145$

我们知道，

中位数 $=l+\frac{\frac{N}{2}-F}{f} \times h$

$=125+\frac{34-22}{20} \times 20$

$=125+12$

$=137$

给定数据的中位数为 137。

上述数据的平均数、众数和中位数分别为 135.07、135.76 和 137。

教程点

更新于： 2022 年 10 月 10 日

151 次查看

开启您的 职业生涯

通过完成课程获得认证

开始学习