Python - 图数据

CSGraph 代表 **压缩稀疏图**，它专注于基于稀疏矩阵表示的快速图算法。

图表示

首先，让我们了解什么是稀疏图以及它如何帮助图表示。

什么是稀疏图？

图只是一组节点，节点之间有链接。图几乎可以表示任何东西——社交网络连接，其中每个节点都是一个人并与其熟人连接；图像，其中每个节点都是一个像素并与其相邻像素连接；高维分布中的点，其中每个节点都与其最近邻连接，以及你能想象到的几乎任何其他东西。

表示图数据的一种非常有效的方法是使用稀疏矩阵：我们称之为 G。矩阵 G 的大小为 N x N，而 G[i, j] 给出节点“i”和节点“j”之间连接的值。稀疏图主要包含零——也就是说，大多数节点只有很少的连接。事实证明，在大多数感兴趣的情况下，此属性都是正确的。

稀疏图子模块的创建受到 scikit-learn 中使用的几种算法的启发，这些算法包括以下内容：

• **Isomap** - 一种流形学习算法，需要在图中找到最短路径。

• **层次聚类** - 一种基于最小生成树的聚类算法。

• **谱分解** - 一种基于稀疏图拉普拉斯算子的投影算法。

作为一个具体的例子，假设我们想表示以下无向图：

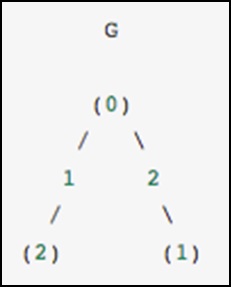
此图具有三个节点，其中节点 0 和 1 通过权重为 2 的边连接，节点 0 和 2 通过权重为 1 的边连接。我们可以构建密集、掩码和稀疏表示，如下例所示，请记住无向图由对称矩阵表示。

G_dense = np.array([ [0, 2, 1],
                     [2, 0, 0],
                     [1, 0, 0] ])
                     
G_masked = np.ma.masked_values(G_dense, 0)
from scipy.sparse import csr_matrix

G_sparse = csr_matrix(G_dense)
print G_sparse.data

上述程序将生成以下输出。

array([2, 1, 2, 1])

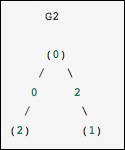
这与前面的图相同，只是节点 0 和 2 通过权重为零的边连接。在这种情况下，上面的密集表示会导致歧义——如果零是有意义的值，如何表示非边。在这种情况下，必须使用掩码或稀疏表示来消除歧义。

让我们考虑以下示例。

from scipy.sparse.csgraph import csgraph_from_dense
G2_data = np.array
([
   [np.inf, 2, 0 ],
   [2, np.inf, np.inf],
   [0, np.inf, np.inf]
])
G2_sparse = csgraph_from_dense(G2_data, null_value=np.inf)
print G2_sparse.data

上述程序将生成以下输出。

array([ 2., 0., 2., 0.])