SciPy - linkage() 方法

---

---

SciPy 的 linkage() 方法用于层次聚类，可用于生成连接矩阵。该矩阵提供了矩阵数据的代码结构。

层次聚类通过将数据分成基于组的方式来定义。以下是数据分析中的两种用途：

• 识别自然分组：它用于借助自然划分来识别分组项。
• 构建树状图：这会创建一个树状图，这是一种树形图，记录数据的分割序列或层次结构。

此方法通常用于数据分析，将相似的项目分组到集群中，这可以帮助我们理解数据的结构并进行预测。

语法

以下是 SciPy linkage() 方法的语法：

linkage(data, method = 'single')
or,
linkage(data, method = 'single', metric = 'type')

参数

此方法接受以下参数：

• data：此参数定义数组形式的数据元素列表。
• method = 'single'：此参数定义链接算法的类型。
• metric = 'type'：默认类型为“欧几里得”。

返回值

此方法返回连接矩阵，其形状为 numpy 数组 (n-1, 4)，其中 n 定义观察次数。

示例 1

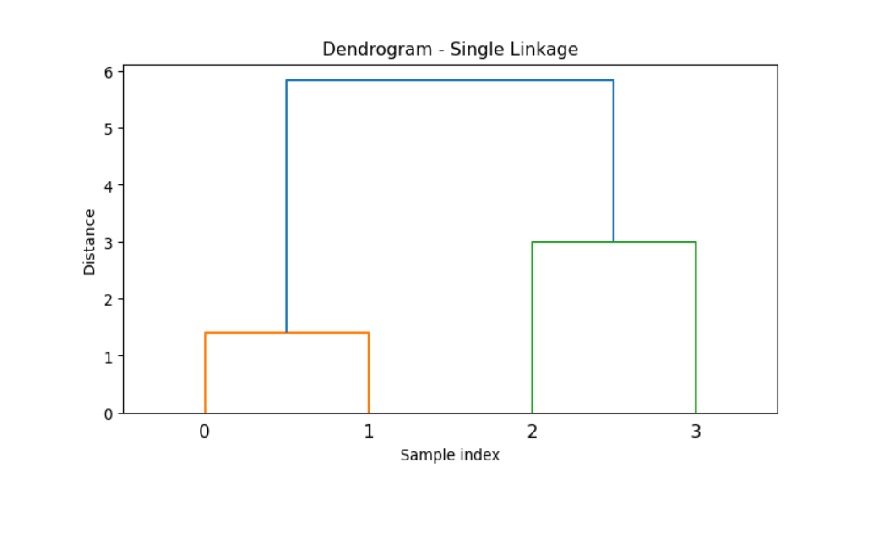
以下是 SciPy linkage() 方法对自定义数据集进行链接聚类，并绘制树状图以可视化数据聚类过程。

import numpy as np
from scipy.cluster.hierarchy import linkage, dendrogram
import matplotlib.pyplot as plt

# Sample data
data = np.array([[1, 2], [2, 3], [5, 8], [8, 8]])

# Compute the linkage matrix using single linkage
result = linkage(data, method='single')

# Plot the dendrogram
plt.figure(figsize=(8, 4))
dendrogram(result)
plt.title('Dendrogram - Single Linkage')
plt.xlabel('Sample index')
plt.ylabel('Distance')
plt.show()

输出

以上代码产生以下结果：

示例 2

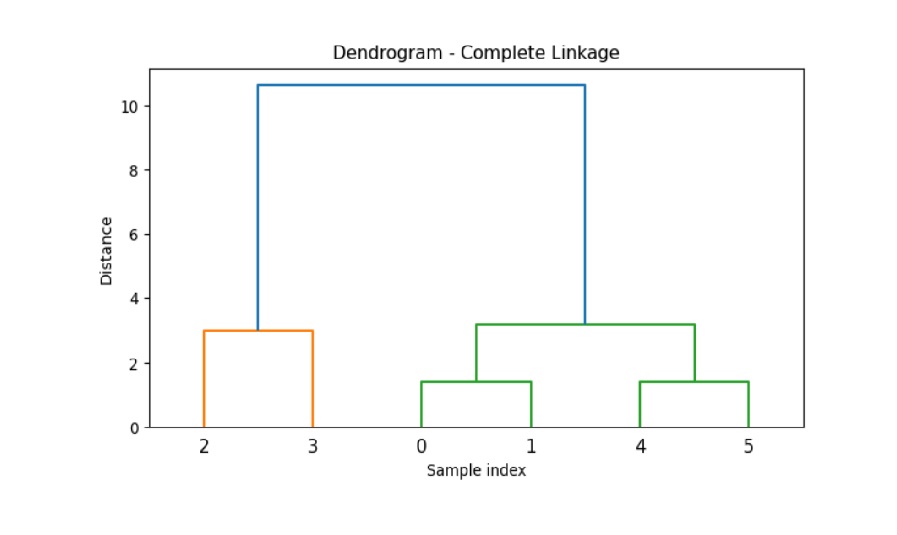
在这里，我们演示了对具有六个观测值的数据集进行完全链接聚类，并使用欧几里得距离度量绘制树状图。

import numpy as np
from scipy.cluster.hierarchy import linkage, dendrogram
import matplotlib.pyplot as plt

# Sample data
data = np.array([[1, 2], [2, 3], [5, 8], [8, 8], [1, 0], [2, 1]])

# Compute the linkage matrix using complete linkage and Euclidean distance
result = linkage(data, method='complete', metric='euclidean')

# Plot the dendrogram
plt.figure(figsize=(8, 4))
dendrogram(result)
plt.title('Dendrogram - Complete Linkage')
plt.xlabel('Sample index')
plt.ylabel('Distance')
plt.show()

输出

以上代码产生以下结果：

示例 3

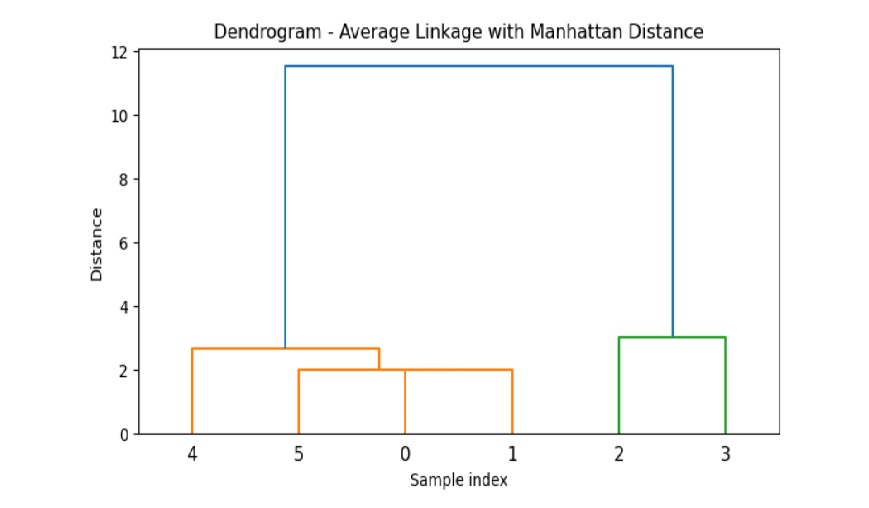
下面的示例使用曼哈顿距离对与示例 2 相同的数据集执行平均链接聚类。这里，它使用度量类型为“cityblock”。

请注意，曼哈顿距离是使用直角的两个点轴测量的。它用于高维数据集。

import numpy as np
from scipy.cluster.hierarchy import linkage, dendrogram
import matplotlib.pyplot as plt

# Sample data
data = np.array([[1, 2], [2, 3], [5, 8], [8, 8], [1, 0], [2, 1]])

# Compute the linkage matrix using average linkage and Manhattan distance
result = linkage(data, method='average', metric='cityblock')

# Plot the dendrogram
plt.figure(figsize=(8, 4))
dendrogram(result)
plt.title('Dendrogram - Average Linkage with Manhattan Distance')
plt.xlabel('Sample index')
plt.ylabel('Distance')
plt.show()

输出

以上代码产生以下结果：