SciPy - 插值

---

---

在本章中，我们将讨论插值如何在 SciPy 中发挥作用。

什么是插值？

插值是在线或曲线上的两点之间查找值的程序。为了帮助我们记住它的含义，我们应该考虑单词的第一部分“inter”，表示“进入”，这提醒我们查看我们最初拥有的数据的“内部”。这种工具，插值，不仅在统计学中很有用，而且在科学、商业或需要预测落在两个现有数据点之间的值时也很有用。

让我们创建一些数据，看看如何使用scipy.interpolate包进行此插值。

import numpy as np
from scipy import interpolate
import matplotlib.pyplot as plt
x = np.linspace(0, 4, 12)
y = np.cos(x**2/3+4)
print x,y

上述程序将生成以下输出。

(
   array([0.,  0.36363636,  0.72727273,  1.09090909,  1.45454545, 1.81818182, 
          2.18181818,  2.54545455,  2.90909091,  3.27272727,  3.63636364,  4.]),
            
   array([-0.65364362,  -0.61966189,  -0.51077021,  -0.31047698,  -0.00715476,
           0.37976236,   0.76715099,   0.99239518,   0.85886263,   0.27994201,
          -0.52586509,  -0.99582185])
)

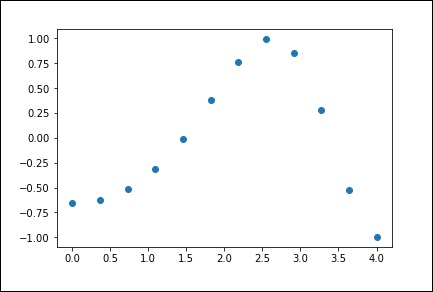
现在，我们有两个数组。假设这两个数组是空间中点的两个维度，让我们使用以下程序进行绘图，看看它们是什么样子。

plt.plot(x, y,’o’)
plt.show()

上述程序将生成以下输出。

一维插值

scipy.interpolate中的interp1d类是一种方便的方法，可以根据固定数据点创建函数，该函数可以使用线性插值在给定数据定义的域内的任何位置进行评估。

使用上述数据，让我们创建一个插值函数并绘制一个新的插值图。

f1 = interp1d(x, y,kind = 'linear')

f2 = interp1d(x, y, kind = 'cubic')

使用interp1d函数，我们创建了两个函数f1和f2。这些函数对于给定的输入x返回y。第三个变量kind表示插值技术的类型。“线性”、“最近”、“零”、“Slinear”、“二次”、“三次”是几种插值技术。

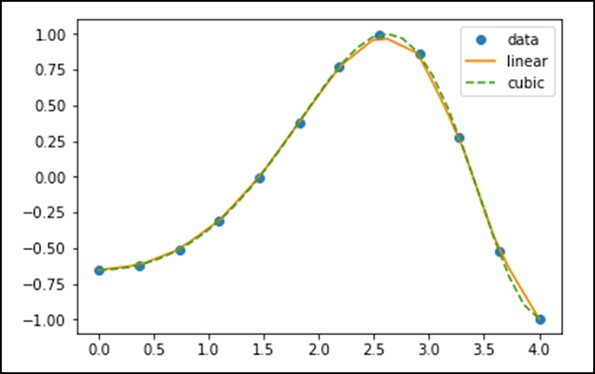
现在，让我们创建一个新的更长的输入来查看插值的明显差异。我们将在新数据上使用旧数据的相同函数。

xnew = np.linspace(0, 4,30)

plt.plot(x, y, 'o', xnew, f(xnew), '-', xnew, f2(xnew), '--')

plt.legend(['data', 'linear', 'cubic','nearest'], loc = 'best')

plt.show()

上述程序将生成以下输出。

样条曲线

为了在数据点之间绘制平滑曲线，绘图员曾经使用称为机械样条的薄而灵活的木条、硬橡胶、金属或塑料条。要使用机械样条，将销钉放置在设计中曲线上的明智选择的点上，然后弯曲样条，使其接触到每个销钉。

显然，通过这种构造，样条曲线在这​​些销钉处对曲线进行插值。它可用于在其他图纸中复制曲线。放置销钉的点称为节点。我们可以通过调整节点的位置来改变样条曲线定义的形状。

单变量样条曲线

一维平滑样条曲线拟合给定的数据集。scipy.interpolate中的UnivariateSpline类是一种方便的方法，可以根据固定数据点创建函数类 - scipy.interpolate.UnivariateSpline(x, y, w = None, bbox = [None, None], k = 3, s = None, ext = 0, check_finite = False)。

参数 - 以下是单变量样条曲线的参数。

• 这将对提供的x、y数据拟合一个度数为k的样条曲线y = spl(x)。

• “w” - 指定样条拟合的权重。必须为正。如果为None（默认值），则所有权重都相等。

• “s” - 通过指定平滑条件来指定节点的数量。

• “k” - 平滑样条的次数。必须<= 5。默认为k = 3，三次样条曲线。

• Ext - 控制不在节点序列定义的区间内的元素的插值模式。

• 如果ext = 0或“extrapolate”，则返回外推值。

• 如果ext = 1或“zero”，则返回0

• 如果ext = 2或“raise”，则引发ValueError

• 如果ext = 3或“const”，则返回边界值。

• check_finite – 是否检查输入数组是否仅包含有限数字。

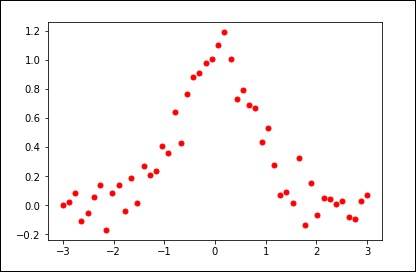
让我们考虑以下示例。

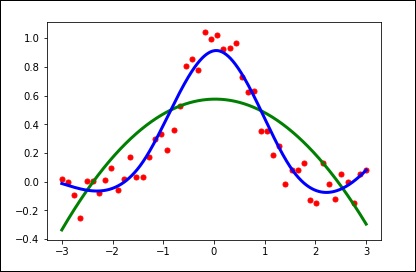
import matplotlib.pyplot as plt
from scipy.interpolate import UnivariateSpline
x = np.linspace(-3, 3, 50)
y = np.exp(-x**2) + 0.1 * np.random.randn(50)
plt.plot(x, y, 'ro', ms = 5)
plt.show()

使用平滑参数的默认值。

spl = UnivariateSpline(x, y)
xs = np.linspace(-3, 3, 1000)
plt.plot(xs, spl(xs), 'g', lw = 3)
plt.show()

手动更改平滑量。

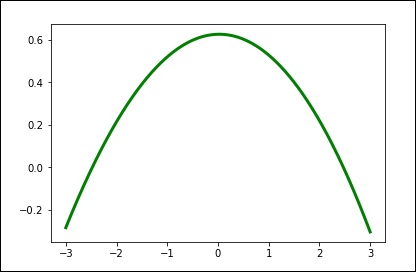
spl.set_smoothing_factor(0.5)
plt.plot(xs, spl(xs), 'b', lw = 3)
plt.show()