
时间序列 - 指数平滑
在本章中,我们将讨论时间序列指数平滑涉及的技术。
简单指数平滑
指数平滑是一种通过对一段时间内的数据分配指数递减的权重来平滑单变量时间序列的技术。
在数学上,给定时间 t 的值,时间 ‘t+1’ 处的变量值 y_(t+1|t) 定义为 -
$$y_{t+1|t}\:=\:\alpha y_{t}\:+\:\alpha\lgroup1 -\alpha\rgroup y_{t-1}\:+\alpha\lgroup1-\alpha\rgroup^{2}\:y_{t-2}\:+\:...+y_{1}$$
其中,$0\leq\alpha \leq1$ 是平滑参数,并且
$y_{1},....,y_{t}$ 是网络流量在时间 1、2、3、…、t 处的先前值。
这是一种对没有明显趋势或季节性的时间序列进行建模的简单方法。但是指数平滑也可以用于具有趋势和季节性的时间序列。
三重指数平滑
三重指数平滑 (TES) 或 Holt-Winters 方法,将指数平滑应用三次 - 水平平滑 $l_{t}$、趋势平滑 $b_{t}$ 和季节性平滑 $S_{t}$,其中 $\alpha$、$\beta^{*}$ 和 $\gamma$ 为平滑参数,‘m’ 为季节频率,即一年中的季节数。
根据季节性成分的性质,TES 有两类 -
Holt-Winters 加法模型 - 当季节性本质上是加法时。
Holt-Winters 乘法模型 - 当季节性本质上是乘法时。
对于非季节性时间序列,我们只有趋势平滑和水平平滑,这称为 Holt 线性趋势方法。
让我们尝试将三重指数平滑应用于我们的数据。
在 [316]
from statsmodels.tsa.holtwinters import ExponentialSmoothing model = ExponentialSmoothing(train.values, trend= ) model_fit = model.fit()
在 [322]
predictions_ = model_fit.predict(len(test))
在 [325]
plt.plot(test.values) plt.plot(predictions_[1:1871])
输出[325]
[<matplotlib.lines.Line2D at 0x1eab00f1cf8>]
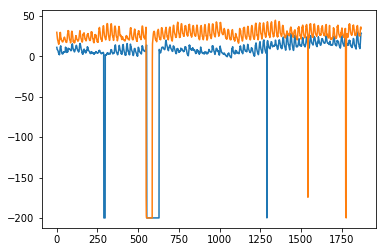
在这里,我们使用训练集训练了一次模型,然后我们继续进行预测。更现实的方法是在一个或多个时间步长后重新训练模型。当我们从训练数据“直到”时间‘t’获得时间‘t+1’的预测时,可以使用训练数据“直到”时间‘t+1’来进行时间‘t+2’的下一个预测,因为此时‘t+1’处的实际值将已知。这种对一个或多个未来步骤进行预测然后重新训练模型的方法称为滚动预测或前向滚动验证。