
时间序列 - LSTM 模型
现在,我们已经熟悉了时间序列上的统计建模,但是机器学习现在非常流行,因此熟悉一些机器学习模型也是必不可少的。我们将从时间序列领域最流行的模型开始——长短期记忆模型。
LSTM 是一种循环神经网络。所以在我们学习 LSTM 之前,必须先了解神经网络和循环神经网络。
神经网络
人工神经网络是由相互连接的神经元组成的分层结构,其灵感来自于生物神经网络。它不是一种算法,而是各种算法的组合,使我们能够对数据进行复杂的运算。
循环神经网络
它是一类专门处理时间序列数据的神经网络。RNN 的神经元具有单元状态/记忆,输入根据这种内部状态进行处理,这是通过神经网络中的循环实现的。RNN 中有重复的“tanh”层模块,使它们能够保留信息。然而,并不能长期保留,这就是为什么我们需要 LSTM 模型。
LSTM
它是一种特殊的循环神经网络,能够学习数据中的长期依赖关系。这是因为模型的循环模块包含四个相互作用的层。
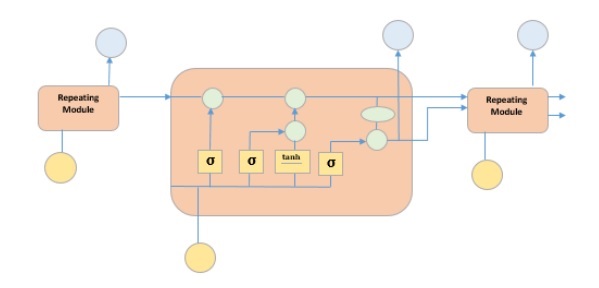
上图描绘了四个用黄色方框表示的神经网络层,绿色圆圈表示逐点运算符,黄色圆圈表示输入,蓝色圆圈表示单元状态。LSTM 模块具有单元状态和三个门,这使它们能够选择性地学习、遗忘或保留来自每个单元的信息。LSTM 中的单元状态通过仅允许少量线性交互来帮助信息在单元之间流动而不会被改变。每个单元都有一个输入门、输出门和一个遗忘门,可以向单元状态添加或删除信息。遗忘门决定应忘记来自先前单元状态的哪些信息,为此它使用 sigmoid 函数。输入门使用“sigmoid”和“tanh”的逐点乘法运算来控制信息流向当前单元状态。最后,输出门决定应将哪些信息传递到下一个隐藏状态。
现在我们已经了解了 LSTM 模型的内部工作原理,让我们来实现它。为了理解 LSTM 的实现,我们将从一个简单的例子开始——一条直线。让我们看看 LSTM 是否能够学习直线的关系并进行预测。
首先,让我们创建一个描述直线的数据集。
代码块 [402]
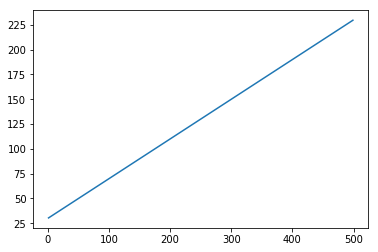
x = numpy.arange (1,500,1) y = 0.4 * x + 30 plt.plot(x,y)
输出 [402]
[<matplotlib.lines.Line2D at 0x1eab9d3ee10>]
代码块 [403]
trainx, testx = x[0:int(0.8*(len(x)))], x[int(0.8*(len(x))):] trainy, testy = y[0:int(0.8*(len(y)))], y[int(0.8*(len(y))):] train = numpy.array(list(zip(trainx,trainy))) test = numpy.array(list(zip(trainx,trainy)))
现在数据已经创建并分成训练集和测试集。让我们根据回溯期的值将时间序列数据转换为监督学习数据的形式,回溯期实质上是预测时间“t”处值的滞后数量。
因此,这样的时间序列:
time variable_x t1 x1 t2 x2 : : : : T xT
当回溯期为 1 时,转换为:
x1 x2 x2 x3 : : : : xT-1 xT
代码块 [404]
def create_dataset(n_X, look_back):
dataX, dataY = [], []
for i in range(len(n_X)-look_back):
a = n_X[i:(i+look_back), ]
dataX.append(a)
dataY.append(n_X[i + look_back, ])
return numpy.array(dataX), numpy.array(dataY)
代码块 [405]
look_back = 1 trainx,trainy = create_dataset(train, look_back) testx,testy = create_dataset(test, look_back) trainx = numpy.reshape(trainx, (trainx.shape[0], 1, 2)) testx = numpy.reshape(testx, (testx.shape[0], 1, 2))
现在我们将训练我们的模型。
将少量训练数据展示给网络,当整个训练数据以批次的形式展示给模型并计算误差时的一次运行称为一个 epoch。epoch 需要运行到误差减少为止。
代码块 []
from keras.models import Sequential
from keras.layers import LSTM, Dense
model = Sequential()
model.add(LSTM(256, return_sequences = True, input_shape = (trainx.shape[1], 2)))
model.add(LSTM(128,input_shape = (trainx.shape[1], 2)))
model.add(Dense(2))
model.compile(loss = 'mean_squared_error', optimizer = 'adam')
model.fit(trainx, trainy, epochs = 2000, batch_size = 10, verbose = 2, shuffle = False)
model.save_weights('LSTMBasic1.h5')
代码块 [407]
model.load_weights('LSTMBasic1.h5')
predict = model.predict(testx)
现在让我们看看我们的预测结果。
代码块 [408]
plt.plot(testx.reshape(398,2)[:,0:1], testx.reshape(398,2)[:,1:2]) plt.plot(predict[:,0:1], predict[:,1:2])
输出 [408]
[<matplotlib.lines.Line2D at 0x1eac792f048>]
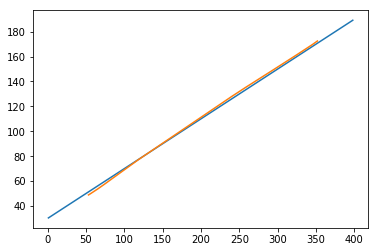
现在,我们应该尝试以类似的方式对正弦波或余弦波进行建模。您可以运行下面给出的代码并调整模型参数以查看结果如何变化。
代码块 [409]
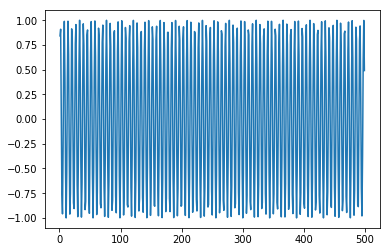
x = numpy.arange (1,500,1) y = numpy.sin(x) plt.plot(x,y)
输出 [409]
[<matplotlib.lines.Line2D at 0x1eac7a0b3c8>]
代码块 [410]
trainx, testx = x[0:int(0.8*(len(x)))], x[int(0.8*(len(x))):] trainy, testy = y[0:int(0.8*(len(y)))], y[int(0.8*(len(y))):] train = numpy.array(list(zip(trainx,trainy))) test = numpy.array(list(zip(trainx,trainy)))
代码块 [411]
look_back = 1 trainx,trainy = create_dataset(train, look_back) testx,testy = create_dataset(test, look_back) trainx = numpy.reshape(trainx, (trainx.shape[0], 1, 2)) testx = numpy.reshape(testx, (testx.shape[0], 1, 2))
代码块 []
model = Sequential()
model.add(LSTM(512, return_sequences = True, input_shape = (trainx.shape[1], 2)))
model.add(LSTM(256,input_shape = (trainx.shape[1], 2)))
model.add(Dense(2))
model.compile(loss = 'mean_squared_error', optimizer = 'adam')
model.fit(trainx, trainy, epochs = 2000, batch_size = 10, verbose = 2, shuffle = False)
model.save_weights('LSTMBasic2.h5')
代码块 [413]
model.load_weights('LSTMBasic2.h5')
predict = model.predict(testx)
代码块 [415]
plt.plot(trainx.reshape(398,2)[:,0:1], trainx.reshape(398,2)[:,1:2]) plt.plot(predict[:,0:1], predict[:,1:2])
输出 [415]
[<matplotlib.lines.Line2D at 0x1eac7a1f550>]
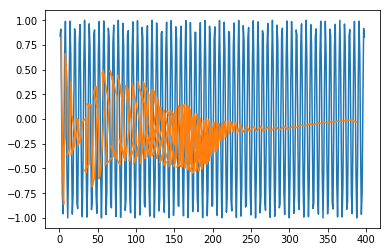
现在您可以开始处理任何数据集了。