时间序列 - 快速指南

时间序列 - 简介

时间序列是在特定时期内的一系列观察值。单变量时间序列由单个变量在一段时间内周期性时间实例中取的值组成，而多变量时间序列由多个变量在一段时间内相同周期性时间实例中取的值组成。我们每天都会遇到的时间序列最简单的例子是全天、一周、一个月或一年的温度变化。

对时间数据的分析能够让我们对变量如何随时间变化，或者它如何依赖于其他变量的值的变化，获得有用的见解。可以分析变量与其先前值和/或其他变量之间的这种关系，用于时间序列预测，并在人工智能中具有众多应用。

时间序列 - 编程语言

对于用户使用或开发机器学习问题，掌握任何编程语言的基本知识都是必不可少的。以下是任何想要从事机器学习工作的人员的首选编程语言列表：

Python

这是一种高级解释型编程语言，快速且易于编码。Python 可以遵循过程式或面向对象的编程范例。各种库的存在使得实现复杂的程序更加简单。在本教程中，我们将使用 Python 编写代码，并在接下来的章节中讨论对时间序列建模有用的相关库。

R

与 Python 类似，R 是一种解释型多范式语言，支持统计计算和图形处理。各种包使得在 R 中实现机器学习建模更加容易。

Java

这是一种解释型面向对象编程语言，因其广泛的包可用性和先进的数据可视化技术而闻名。

C/C++

这些是编译型语言，也是两种最古老的编程语言。这些语言通常被用来将机器学习功能整合到现有的应用程序中，因为它们允许您轻松地定制机器学习算法的实现。

MATLAB

MATrix LABoratory 是一种多范式语言，它提供了处理矩阵的功能。它允许对复杂问题进行数学运算。它主要用于数值运算，但一些包也允许图形化多域仿真和基于模型的设计。

其他首选用于机器学习问题的编程语言包括 JavaScript、LISP、Prolog、SQL、Scala、Julia、SAS 等。

时间序列 - Python 库

由于其易于编写和理解的代码结构以及各种开源库，Python 在进行机器学习的个人中享有盛誉。我们在接下来的章节中将使用的一些此类开源库已在下面介绍。

NumPy

Numerical Python 是一个用于科学计算的库。它基于 N 维数组对象，并提供基本数学功能，例如大小、形状、均值、标准差、最小值、最大值，以及一些更复杂的功能，例如线性代数函数和傅里叶变换。随着我们在这个教程中继续学习，您将了解更多关于这些内容。

Pandas

这个库提供了高效且易于使用的数据结构，例如序列、数据框和面板。它增强了 Python 的功能，从单纯的数据收集和准备到数据分析。Pandas 和 NumPy 这两个库使得对小型到超大型数据集的任何操作都非常简单。要了解有关这些功能的更多信息，请遵循本教程。

SciPy

Science Python 是一个用于科学和技术计算的库。它提供了优化、信号和图像处理、积分、插值和线性代数的功能。在执行机器学习时，这个库非常方便。随着我们在这个教程中继续学习，我们将讨论这些功能。

Scikit-learn

这个库是一个 SciPy 工具包，广泛用于统计建模、机器学习和深度学习，因为它包含各种可定制的回归、分类和聚类模型。它与 NumPy、Pandas 和其他库配合良好，使其更容易使用。

Statsmodels

与 Scikit-learn 类似，这个库用于统计数据探索和统计建模。它也与其他 Python 库配合良好。

Matplotlib

这个库用于以各种格式（例如线图、条形图、热图、散点图、直方图等）进行数据可视化。它包含从绘图到标签的所有图形相关功能。随着我们在这个教程中继续学习，我们将讨论这些功能。

这些库对于开始使用任何类型的数据进行机器学习非常重要。

除了上面讨论的库之外，另一个特别重要用于处理时间序列的库是：

Datetime

这个库及其两个模块（datetime 和 calendar）提供了读取、格式化和处理时间所需的所有 datetime 功能。

我们将在接下来的章节中使用这些库。

时间序列 - 数据处理和可视化

时间序列是在等间距时间间隔内索引的一系列观测值。因此，在任何时间序列中都应保持顺序和连续性。

我们将使用的数据集是一个多变量时间序列，包含大约一年的某个严重污染的意大利城市空气质量的小时数据。数据集可以从以下链接下载：https://archive.ics.uci.edu/ml/datasets/air+quality。

有必要确保：

时间序列是等间距的，并且
其中没有冗余值或缺口。

如果时间序列不连续，我们可以对其进行上采样或下采样。

显示 df.head()

In [122]

import pandas

In [123]

df = pandas.read_csv("AirQualityUCI.csv", sep = ";", decimal = ",")
df = df.iloc[ : , 0:14]

In [124]

len(df)

Out[124]

In [125]

df.head()

Out[125]

为了预处理时间序列，我们确保数据集中没有 NaN（NULL）值；如果有，我们可以将它们替换为 0 或平均值或前一个或后一个值。替换比删除更可取，这样可以保持时间序列的连续性。但是，在我们的数据集中，最后几个值似乎是 NULL，因此删除不会影响连续性。

删除 NaN（非数字）

In [126]

df.isna().sum()
Out[126]:
Date             114
Time             114
CO(GT)           114
PT08.S1(CO)      114
NMHC(GT)         114
C6H6(GT)         114
PT08.S2(NMHC)    114
NOx(GT)          114
PT08.S3(NOx)     114
NO2(GT)          114
PT08.S4(NO2)     114
PT08.S5(O3)      114
T                114
RH               114
dtype: int64

In [127]

df = df[df['Date'].notnull()]

In [128]

df.isna().sum()

Out[128]

Date             0
Time             0
CO(GT)           0
PT08.S1(CO)      0
NMHC(GT)         0
C6H6(GT)         0
PT08.S2(NMHC)    0
NOx(GT)          0
PT08.S3(NOx)     0
NO2(GT)          0
PT08.S4(NO2)     0
PT08.S5(O3)      0
T                0
RH               0
dtype: int64

时间序列通常以线图的形式相对于时间绘制。为此，我们现在将合并日期和时间列，并将其从字符串转换为 datetime 对象。这可以使用 datetime 库来完成。

转换为 datetime 对象

In [129]

df['DateTime'] = (df.Date) + ' ' + (df.Time)
print (type(df.DateTime[0]))

<class 'str'>

In [130]

import datetime

df.DateTime = df.DateTime.apply(lambda x: datetime.datetime.strptime(x, '%d/%m/%Y %H.%M.%S'))
print (type(df.DateTime[0]))

让我们看看一些变量（如温度）如何随着时间的变化而变化。

显示图表

In [131]

df.index = df.DateTime

In [132]

import matplotlib.pyplot as plt
plt.plot(df['T'])

Out[132]

[<matplotlib.lines.Line2D at 0x1eaad67f780>]

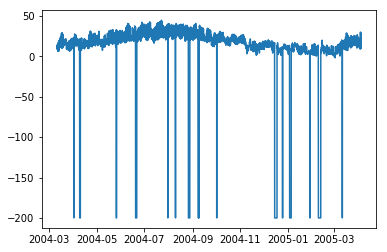
In [208]

plt.plot(df['C6H6(GT)'])

Out[208]

[<matplotlib.lines.Line2D at 0x1eaaeedff28>]

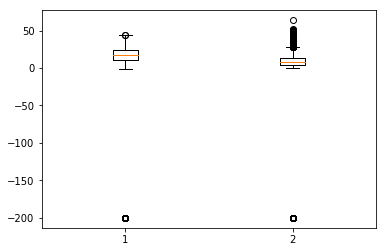
箱线图是另一种有用的图表类型，它允许您将大量有关数据集的信息压缩到单个图表中。它显示了一个或多个变量的均值、25% 和 75% 分位数以及异常值。当异常值数量很少且与均值相距甚远时，我们可以通过将异常值设置为均值或 75% 分位数值来消除异常值。

显示箱线图

In [134]

plt.boxplot(df[['T','C6H6(GT)']].values)

Out[134]

{'whiskers': [<matplotlib.lines.Line2D at 0x1eaac16de80>,
   <matplotlib.lines.Line2D at 0x1eaac16d908>,
   <matplotlib.lines.Line2D at 0x1eaac177a58>,
   <matplotlib.lines.Line2D at 0x1eaac177cf8>],
   'caps': [<matplotlib.lines.Line2D at 0x1eaac16d2b0>,
   <matplotlib.lines.Line2D at 0x1eaac16d588>,
   <matplotlib.lines.Line2D at 0x1eaac1a69e8>,
   <matplotlib.lines.Line2D at 0x1eaac1a64a8>],
   'boxes': [<matplotlib.lines.Line2D at 0x1eaac16dc50>,
   <matplotlib.lines.Line2D at 0x1eaac1779b0>],
   'medians': [<matplotlib.lines.Line2D at 0x1eaac16d4a8>,
   <matplotlib.lines.Line2D at 0x1eaac1a6c50>],
   'fliers': [<matplotlib.lines.Line2D at 0x1eaac177dd8>,
   <matplotlib.lines.Line2D at 0x1eaac1a6c18>],'means': []
}

时间序列 - 建模

简介

时间序列具有以下四个组成部分：

水平 - 它是级数变化的平均值。
趋势 - 它是变量随时间增加或减少的行为。
季节性 - 它是时间序列的周期性行为。
噪声 - 这是由于环境因素而添加到观测值中的误差。

时间序列建模技术

为了捕捉这些组成部分，有很多流行的时间序列建模技术。本节简要介绍了每种技术，但是我们将在接下来的章节中详细讨论它们：

朴素方法

这些是简单的估计技术，例如，预测值等于时间相关变量的前一个值的均值或前一个实际值。这些用于与复杂的建模技术进行比较。

自回归

自回归将未来时间段的值预测为先前时间段的值的函数。自回归的预测可能比朴素方法更能拟合数据，但它可能无法解释季节性。

ARIMA 模型

自回归积分移动平均模型将变量的值建模为平稳时间序列先前值的线性函数和先前时间步长的残差误差。然而，现实世界的数据可能是非平稳的并且具有季节性，因此开发了季节性 ARIMA 和分数 ARIMA。ARIMA 用于单变量时间序列，为了处理多个变量，引入了 VARIMA。

指数平滑

它将变量的值建模为先前值的指数加权线性函数。该统计模型也可以处理趋势和季节性。

LSTM

长短期记忆模型 (LSTM) 是一种循环神经网络，用于时间序列以解释长期依赖关系。它可以用大量数据进行训练以捕获多变量时间序列中的趋势。

上述建模技术用于时间序列回归。在接下来的章节中，让我们逐一探索所有这些。

时间序列 - 参数校准

简介

任何统计或机器学习模型都有一些参数，这些参数极大地影响了数据的建模方式。例如，ARIMA 具有 p、d、q 值。这些参数的确定应使实际值与建模值之间的误差最小。参数校准可以说是模型拟合中最关键和最耗时的任务。因此，为我们选择最佳参数非常重要。

参数校准方法

有多种方法可以校准参数。本节将详细介绍其中一些方法。

反复试验

一种常见的模型校准方法是手动校准，您从可视化时间序列开始，直观地尝试一些参数值，并反复更改它们，直到达到足够好的拟合度。这需要对我们正在尝试的模型有很好的理解。对于 ARIMA 模型，手动校准是借助自相关图来确定“p”参数，偏自相关图来确定“q”参数，ADF 检验来确认时间序列的平稳性并设置“d”参数来完成的。我们将在接下来的章节中详细讨论所有这些。

网格搜索

另一种模型校准方法是网格搜索，这实质上意味着您尝试为所有可能的参数组合构建模型，并选择误差最小的模型。这很耗时，因此当要校准的参数数量和它们取值的范围较少时很有用，因为这涉及多个嵌套的 for 循环。

遗传算法

遗传算法基于生物学原理，即好的解决方案最终会进化到最“优”的解决方案。它使用生物学中的突变、交叉和选择操作最终达到最优解。

要了解更多知识，您可以阅读其他参数优化技术，例如贝叶斯优化和群体智能优化。

时间序列 - 朴素方法

简介

朴素方法，例如假设t时刻的预测值等于t-1时刻变量的实际值，或使用序列的移动平均值，用于衡量统计模型和机器学习模型的性能，并强调它们的必要性。

在本章中，让我们尝试将这些模型应用于时间序列数据的一个特征。

首先，我们将查看数据中“温度”特征的均值及其周围的偏差。查看最高和最低温度值也很有用。这里可以使用numpy库的功能。

显示统计数据

In [135]

import numpy
print (
   'Mean: ',numpy.mean(df['T']), '; 
   Standard Deviation: ',numpy.std(df['T']),'; 
   \nMaximum Temperature: ',max(df['T']),'; 
   Minimum Temperature: ',min(df['T'])
)

我们获得了9357个观测值在等间隔时间线上的统计数据，这些数据有助于我们理解数据。

现在我们将尝试第一种朴素方法，将当前时刻的预测值设置为前一时刻的实际值，并计算其均方根误差 (RMSE) 以量化该方法的性能。

显示第一种朴素方法

In [136]

df['T']
df['T_t-1'] = df['T'].shift(1)

In [137]

df_naive = df[['T','T_t-1']][1:]

In [138]

from sklearn import metrics
from math import sqrt

true = df_naive['T']
prediction = df_naive['T_t-1']
error = sqrt(metrics.mean_squared_error(true,prediction))
print ('RMSE for Naive Method 1: ', error)

朴素方法 1 的 RMSE：12.901140576492974

让我们看看下一个朴素方法，其中当前时刻的预测值等于其之前时间段的平均值。我们也将计算此方法的RMSE。

显示第二种朴素方法

In [139]

df['T_rm'] = df['T'].rolling(3).mean().shift(1)
df_naive = df[['T','T_rm']].dropna()

In [140]

true = df_naive['T']
prediction = df_naive['T_rm']
error = sqrt(metrics.mean_squared_error(true,prediction))
print ('RMSE for Naive Method 2: ', error)

朴素方法 2 的 RMSE：14.957633272839242

在这里，您可以尝试不同的先前时间段数，也称为“滞后”，这里设置为3。在这个数据集中可以看出，随着滞后数量的增加，误差也会增加。如果滞后设置为1，它就与之前使用的朴素方法相同。

注意事项

您可以编写一个非常简单的函数来计算均方根误差。这里，我们使用了'sklearn'包中的均方误差函数，然后取其平方根。
在pandas中，df['column_name']也可以写成df.column_name，但是对于这个数据集，df.T与df['T']的作用不同，因为df.T是转置数据框的函数。因此，只使用df['T']或考虑在使用其他语法之前重命名此列。

时间序列 - 自回归

对于平稳时间序列，自回归模型将t时刻变量的值视为其前p个时间步长的值的线性函数。数学上可以写成：

$$y_{t} = \:C+\:\phi_{1}y_{t-1}\:+\:\phi_{2}Y_{t-2}+...+\phi_{p}y_{t-p}+\epsilon_{t}$$

其中，‘p’是自回归趋势参数

$\epsilon_{t}$是白噪声，并且

$y_{t-1}, y_{t-2}\:\: ...y_{t-p}$表示变量在先前时间段的值。

p的值可以使用各种方法进行校准。找到合适的'p'值的一种方法是绘制自相关图。

注意 - 在对数据进行任何分析之前，我们应该将数据按照8:2的比例分成训练集和测试集，因为测试数据仅用于找出模型的准确性，并且假设在我们做出预测之后才能获得测试数据。在时间序列的情况下，数据点的顺序非常重要，因此在分割数据时应注意不要丢失顺序。

自相关图或相关图显示了变量与其自身在先前时间步长的关系。它利用皮尔逊相关系数，并显示95%置信区间内的相关性。让我们看看它在我们的数据“温度”变量中的样子。

显示自相关图

In [141]

split = len(df) - int(0.2*len(df))
train, test = df['T'][0:split], df['T'][split:]

In [142]

from statsmodels.graphics.tsaplots import plot_acf

plot_acf(train, lags = 100)
plt.show()

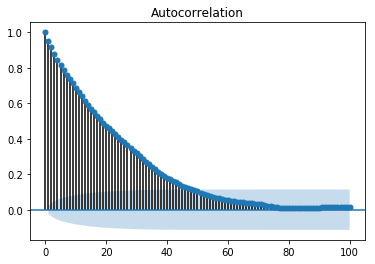
所有位于蓝色阴影区域之外的滞后值都被认为具有相关性。

时间序列 - 移动平均

对于平稳时间序列，移动平均模型将t时刻变量的值视为其前q个时间步长的残差误差的线性函数。残差误差是通过将t时刻的值与之前值的移动平均值进行比较来计算的。

数学上可以写成：

$$y_{t} = c\:+\:\epsilon_{t}\:+\:\theta_{1}\:\epsilon_{t-1}\:+\:\theta_{2}\:\epsilon_{t-2}\:+\:...+:\theta_{q}\:\epsilon_{t-q}\:$$

其中‘q’是移动平均趋势参数

$\epsilon_{t}$是白噪声，并且

$\epsilon_{t-1}, \epsilon_{t-2}...\epsilon_{t-q}$是先前时间段的误差项。

可以使用各种方法校准'q'的值。找到合适的'q'值的一种方法是绘制偏自相关图。

偏自相关图显示了变量与其自身在先前时间步长的关系，消除了间接相关性，这与显示直接和间接相关性的自相关图不同，让我们看看它在我们的数据“温度”变量中的样子。

显示偏自相关图

In [143]

from statsmodels.graphics.tsaplots import plot_pacf

plot_pacf(train, lags = 100)
plt.show()

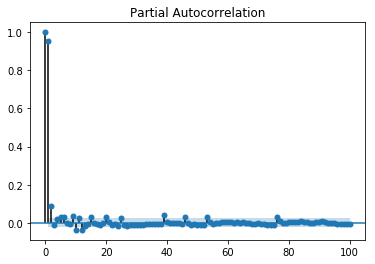
偏自相关图的解读方式与相关图相同。

时间序列 - ARIMA

我们已经了解到，对于平稳时间序列，t时刻的变量是先前观测值或残差误差的线性函数。因此，现在是时候将两者结合起来，形成自回归移动平均 (ARMA) 模型了。

然而，有时时间序列不是平稳的，即序列的统计特性（如均值、方差）会随时间变化。而我们迄今为止研究的统计模型都假设时间序列是平稳的，因此，我们可以加入一个对时间序列进行差分以使其平稳的预处理步骤。现在，重要的是我们要找出我们正在处理的时间序列是否平稳。

查找时间序列平稳性的各种方法包括：观察时间序列图中的季节性或趋势，检查不同时间段的均值和方差差异，增广迪基-福勒 (ADF) 检验，KPSS 检验，赫斯特指数等。

让我们使用 ADF 检验看看我们数据集的“温度”变量是否是平稳时间序列。

In [74]

from statsmodels.tsa.stattools import adfuller

result = adfuller(train)
print('ADF Statistic: %f' % result[0])
print('p-value: %f' % result[1])
print('Critical Values:')
for key, value In result[4].items()
   print('\t%s: %.3f' % (key, value))

ADF 统计量：-10.406056

p 值：0.000000

临界值

1%: -3.431

5%: -2.862

10%: -2.567

既然我们已经运行了 ADF 检验，让我们解释一下结果。首先，我们将 ADF 统计量与临界值进行比较，较低的临界值告诉我们该序列很可能是非平稳的。接下来，我们查看 p 值。p 值大于 0.05 也表明时间序列是非平稳的。

或者，p 值小于或等于 0.05，或 ADF 统计量小于临界值，表明时间序列是平稳的。

因此，我们正在处理的时间序列已经是平稳的了。对于平稳时间序列，我们将'd'参数设置为0。

我们也可以使用赫斯特指数来确认时间序列的平稳性。

In [75]

import hurst

H, c,data = hurst.compute_Hc(train)
print("H = {:.4f}, c = {:.4f}".format(H,c))

H = 0.1660，c = 5.0740

H<0.5 表示反持久性行为，H>0.5 表示持久性行为或趋势序列。H=0.5 表示随机游走/布朗运动。H<0.5 的值证实了我们的序列是平稳的。

对于非平稳时间序列，我们将'd'参数设置为1。此外，自回归趋势参数'p'和移动平均趋势参数'q'是在平稳时间序列上计算的，即通过对时间序列进行差分后绘制自相关图和偏自相关图来计算。

ARIMA 模型由三个参数 (p,d,q) 构成，现在我们已经清楚了，所以让我们对我们的时间序列进行建模并预测未来的温度值。

In [156]

from statsmodels.tsa.arima_model import ARIMA

model = ARIMA(train.values, order=(5, 0, 2))
model_fit = model.fit(disp=False)

In [157]

predictions = model_fit.predict(len(test))
test_ = pandas.DataFrame(test)
test_['predictions'] = predictions[0:1871]

In [158]

plt.plot(df['T'])
plt.plot(test_.predictions)
plt.show()

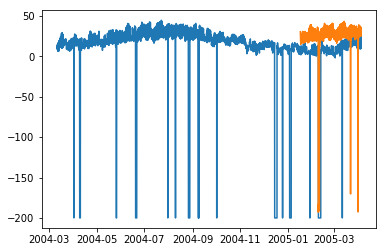
In [167]

error = sqrt(metrics.mean_squared_error(test.values,predictions[0:1871]))
print ('Test RMSE for ARIMA: ', error)

ARIMA 模型的测试 RMSE：43.21252940234892

时间序列 - ARIMA 的变体

在上一章中，我们已经了解了 ARIMA 模型的工作原理及其局限性，即它无法处理季节性数据或多元时间序列，因此，引入了新的模型来包含这些特征。

这里简要介绍一下这些新模型：

向量自回归 (VAR)

它是多元平稳时间序列的自回归模型的推广版本。它由'p'参数构成。

向量移动平均 (VMA)

它是多元平稳时间序列的移动平均模型的推广版本。它由'q'参数构成。

向量自回归移动平均 (VARMA)

它是 VAR 和 VMA 的组合，也是多元平稳时间序列的 ARMA 模型的推广版本。它由'p'和'q'参数构成。就像 ARMA 可以通过将'q'参数设置为0来充当 AR 模型，通过将'p'参数设置为0来充当 MA 模型一样，VARMA 也能够通过将'q'参数设置为0来充当 VAR 模型，通过将'p'参数设置为0来充当 VMA 模型。

In [209]

df_multi = df[['T', 'C6H6(GT)']]
split = len(df) - int(0.2*len(df))
train_multi, test_multi = df_multi[0:split], df_multi[split:]

In [211]

from statsmodels.tsa.statespace.varmax import VARMAX

model = VARMAX(train_multi, order = (2,1))
model_fit = model.fit()
c:\users\naveksha\appdata\local\programs\python\python37\lib\site-packages\statsmodels\tsa\statespace\varmax.py:152: 
   EstimationWarning: Estimation of VARMA(p,q) models is not generically robust, 
   due especially to identification issues. 
   EstimationWarning)
c:\users\naveksha\appdata\local\programs\python\python37\lib\site-packages\statsmodels\tsa\base\tsa_model.py:171: 
   ValueWarning: No frequency information was provided, so inferred frequency H will be used. 
  % freq, ValueWarning)
c:\users\naveksha\appdata\local\programs\python\python37\lib\site-packages\statsmodels\base\model.py:508: 
   ConvergenceWarning: Maximum Likelihood optimization failed to converge. Check mle_retvals 
  "Check mle_retvals", ConvergenceWarning)

In [213]

predictions_multi = model_fit.forecast( steps=len(test_multi))
c:\users\naveksha\appdata\local\programs\python\python37\lib\site-packages\statsmodels\tsa\base\tsa_model.py:320: 
   FutureWarning: Creating a DatetimeIndex by passing range endpoints is deprecated.  Use `pandas.date_range` instead.
   freq = base_index.freq)
c:\users\naveksha\appdata\local\programs\python\python37\lib\site-packages\statsmodels\tsa\statespace\varmax.py:152: 
   EstimationWarning: Estimation of VARMA(p,q) models is not generically robust, due especially to identification issues.
   EstimationWarning)

In [231]

plt.plot(train_multi['T'])
plt.plot(test_multi['T'])
plt.plot(predictions_multi.iloc[:,0:1], '--')
plt.show()

plt.plot(train_multi['C6H6(GT)'])
plt.plot(test_multi['C6H6(GT)'])
plt.plot(predictions_multi.iloc[:,1:2], '--')
plt.show()

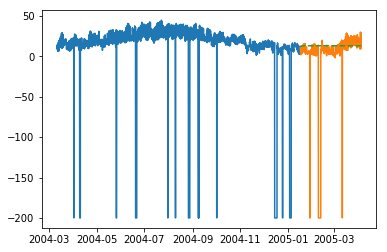
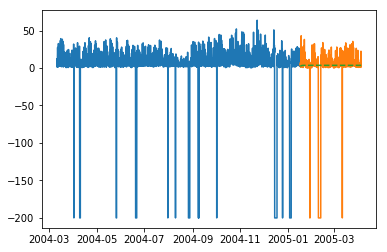
上述代码显示了如何使用 VARMA 模型对多元时间序列进行建模，尽管该模型可能不适合我们的数据。

具有外生变量的 VARMA (VARMAX)

它是 VARMA 模型的扩展，其中使用称为协变量的额外变量来模拟我们感兴趣的主要变量。

季节性自回归积分移动平均 (SARIMA)

这是 ARIMA 模型的扩展，用于处理季节性数据。它将数据分为季节性和非季节性成分，并以类似的方式对它们进行建模。它由7个参数构成，非季节性部分 (p,d,q) 参数与 ARIMA 模型相同，季节性部分 (P,D,Q,m) 参数中'm'是季节周期数，P,D,Q与 ARIMA 模型的参数类似。这些参数可以使用网格搜索或遗传算法进行校准。

具有外生变量的 SARIMA (SARIMAX)

这是 SARIMA 模型的扩展，其中包含有助于我们对感兴趣的变量进行建模的外生变量。

在将变量作为外生变量输入之前，进行变量的相关性分析可能会有用。

In [251]

from scipy.stats.stats import pearsonr
x = train_multi['T'].values
y = train_multi['C6H6(GT)'].values

corr , p = pearsonr(x,y)
print ('Corelation Coefficient =', corr,'\nP-Value =',p)
Corelation Coefficient = 0.9701173437269858
P-Value = 0.0

皮尔逊相关系数显示了两个变量之间的线性关系，为了解释结果，我们首先查看 p 值，如果它小于 0.05，则系数的值是显著的，否则系数的值是不显著的。对于显著的 p 值，正的相关系数值表示正相关，负的值表示负相关。

因此，对于我们的数据，“温度”和“C6H6”似乎具有高度的正相关性。因此，我们将

In [297]

from statsmodels.tsa.statespace.sarimax import SARIMAX

model = SARIMAX(x, exog = y, order = (2, 0, 2), seasonal_order = (2, 0, 1, 1), enforce_stationarity=False, enforce_invertibility = False)
model_fit = model.fit(disp = False)
c:\users\naveksha\appdata\local\programs\python\python37\lib\site-packages\statsmodels\base\model.py:508: 
   ConvergenceWarning: Maximum Likelihood optimization failed to converge. Check mle_retvals
   "Check mle_retvals", ConvergenceWarning)

In [298]

y_ = test_multi['C6H6(GT)'].values
predicted = model_fit.predict(exog=y_)
test_multi_ = pandas.DataFrame(test)
test_multi_['predictions'] = predicted[0:1871]

In [299]

plt.plot(train_multi['T'])
plt.plot(test_multi_['T'])
plt.plot(test_multi_.predictions, '--')

Out[299]

[<matplotlib.lines.Line2D at 0x1eab0191c18>]

与单变量 ARIMA 建模相比，这里的预测现在似乎有更大的变化。

不用说，SARIMAX 可以通过将相应的参数设置为非零值来用作 ARX、MAX、ARMAX 或 ARIMAX 模型。

分数自回归积分移动平均模型 (FARIMA)

有时，我们的序列可能不是平稳的，但使用参数‘d’取值为1进行差分可能会过度差分。因此，我们需要使用分数值对时间序列进行差分。

在数据科学领域，没有一个最优模型，哪个模型适合你的数据很大程度上取决于你的数据集。了解各种模型使我们能够选择一个适用于我们数据的模型，并通过试验该模型来获得最佳结果。结果应该以图表和误差指标的形式呈现，有时即使是很小的误差也可能是坏的，因此，绘制和可视化结果至关重要。

在下一章中，我们将研究另一个统计模型：指数平滑。

时间序列 - 指数平滑

在本章中，我们将讨论时间序列指数平滑涉及的技术。

简单指数平滑

指数平滑是一种通过对一段时间内的数据赋予指数递减的权重来平滑单变量时间序列的技术。

数学上，给定时间t的值，时间‘t+1’时变量的值 y_(t+1|t) 定义为：

$$y_{t+1|t}\:=\:\alpha y_{t}\:+\:\alpha\lgroup1 -\alpha\rgroup y_{t-1}\:+\alpha\lgroup1-\alpha\rgroup^{2}\:y_{t-2}\:+\:...+y_{1}$$

其中，$0\leq\alpha \leq1$ 是平滑参数，并且

$y_{1},....,y_{t}$ 是网络流量在时间1、2、3、……、t之前的数值。

这是一种对没有明显趋势或季节性的时间序列进行建模的简单方法。但是指数平滑也可以用于具有趋势和季节性的时间序列。

三重指数平滑

三重指数平滑 (TES) 或 Holt-Winters 方法，将指数平滑应用三次——水平平滑 $l_{t}$、趋势平滑 $b_{t}$ 和季节性平滑 $S_{t}$，其中 $\alpha$、$\beta^{*}$ 和 $\gamma$ 为平滑参数，‘m’为季节性频率，即一年中的季节数。

根据季节性成分的性质，TES 有两类：

Holt-Winters 加法模型——当季节性是加法性质时。
Holt-Winters 乘法模型——当季节性是乘法性质时。

对于非季节性时间序列，我们只有趋势平滑和水平平滑，这被称为 Holt 的线性趋势法。

让我们尝试将三重指数平滑应用于我们的数据。

代码块 [316]

from statsmodels.tsa.holtwinters import ExponentialSmoothing

model = ExponentialSmoothing(train.values, trend= )
model_fit = model.fit()

代码块 [322]

predictions_ = model_fit.predict(len(test))

代码块 [325]

plt.plot(test.values)
plt.plot(predictions_[1:1871])

输出 [325]

[<matplotlib.lines.Line2D at 0x1eab00f1cf8>]

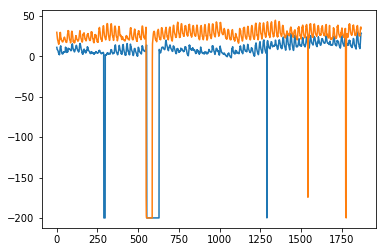
在这里，我们已经使用训练集训练过一次模型，然后我们继续进行预测。更现实的方法是在一个或多个时间步长后重新训练模型。当我们从训练数据（直到时间‘t’）中获得时间‘t+1’的预测值时，下一个时间‘t+2’的预测可以使用直到时间‘t+1’的训练数据进行，因为此时‘t+1’的实际值将已知。这种对一个或多个未来步骤进行预测然后重新训练模型的方法称为滚动预测或前滚验证。

时间序列 - 前向验证

在时间序列建模中，随着时间的推移，预测变得越来越不准确，因此，随着实际数据的可用性，使用实际数据重新训练模型以进行进一步预测是一种更现实的方法。由于统计模型的训练不耗时，因此前滚验证是获得最准确结果的首选解决方案。

让我们对我们的数据应用一步前滚验证，并将其与我们之前获得的结果进行比较。

代码块 [333]

prediction = []
data = train.values
for t In test.values:
   model = (ExponentialSmoothing(data).fit())
   y = model.predict()
   prediction.append(y[0])
   data = numpy.append(data, t)

代码块 [335]

test_ = pandas.DataFrame(test)
test_['predictionswf'] = prediction

代码块 [341]

plt.plot(test_['T'])
plt.plot(test_.predictionswf, '--')
plt.show()

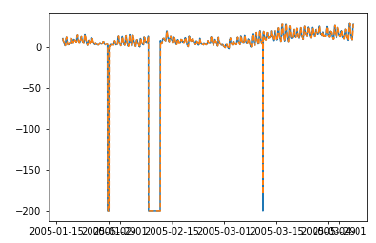
代码块 [340]

error = sqrt(metrics.mean_squared_error(test.values,prediction))
print ('Test RMSE for Triple Exponential Smoothing with Walk-Forward Validation: ', error)
Test RMSE for Triple Exponential Smoothing with Walk-Forward Validation:  11.787532205759442

我们可以看到，我们的模型现在性能明显更好。事实上，趋势跟踪得如此紧密，以至于在图中预测值与实际值重叠。你也可以尝试将前滚验证应用于 ARIMA 模型。

时间序列 - Prophet 模型

2017年，Facebook 开源了 Prophet 模型，该模型能够对具有强多重季节性（日级、周级、年级等）和趋势的时间序列进行建模。它具有直观的参数，即使不是专家级别的数据科学家也可以调整这些参数以获得更好的预测结果。其核心是一个加性回归模型，可以检测变化点以对时间序列进行建模。

Prophet 将时间序列分解成趋势 $g_{t}$、季节性 $S_{t}$ 和节假日 $h_{t}$ 的组成部分。

$$y_{t}=g_{t}+s_{t}+h_{t}+\epsilon_{t}$$

其中，$\epsilon_{t}$ 是误差项。

谷歌和推特分别在 R 中引入了类似的时间序列预测包，例如因果影响和异常检测。

时间序列 - LSTM 模型

现在，我们已经熟悉了时间序列的统计建模，但是机器学习现在非常流行，因此熟悉一些机器学习模型也很重要。我们将从时间序列领域最流行的模型开始——长短期记忆模型。

LSTM 是一种循环神经网络。所以在我们学习 LSTM 之前，了解神经网络和循环神经网络是必要的。

神经网络

人工神经网络是由相互连接的神经元组成的分层结构，其灵感来自于生物神经网络。它不是一种算法，而是各种算法的组合，使我们能够对数据进行复杂的操作。

循环神经网络

它是一种专门处理时间序列数据的神经网络。RNN 的神经元具有单元状态/记忆，输入根据这种内部状态进行处理，这是通过神经网络中的循环实现的。RNN 中有重复的“tanh”层模块，允许它们保留信息。然而，不能长期保留，这就是我们需要 LSTM 模型的原因。

LSTM

它是一种特殊的循环神经网络，能够学习数据中的长期依赖关系。这是因为模型的重复模块包含四个相互作用的层。

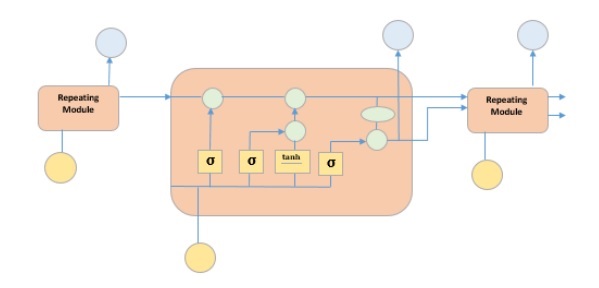
上图描绘了黄框中的四个神经网络层，绿圈中的逐点运算符，黄圈中的输入和蓝圈中的单元状态。LSTM 模块具有单元状态和三个门，这使它们能够选择性地学习、遗忘或保留来自每个单元的信息。LSTM 中的单元状态通过只允许少量线性交互来帮助信息在单元之间流动而不会被改变。每个单元都有一个输入门、输出门和一个遗忘门，它们可以向单元状态添加或删除信息。遗忘门决定应该忘记来自先前单元状态的哪些信息，为此它使用 sigmoid 函数。输入门使用“sigmoid”和“tanh”的逐点乘法运算分别控制信息流向当前单元状态。最后，输出门决定应该将哪些信息传递给下一个隐藏状态。

现在我们已经了解了 LSTM 模型的内部工作原理，让我们来实现它。为了理解 LSTM 的实现，我们将从一个简单的例子开始——一条直线。让我们看看 LSTM 是否能够学习直线的规律并对其进行预测。

首先让我们创建一个描绘直线的数据集。

代码块 [402]

x = numpy.arange (1,500,1)
y = 0.4 * x + 30
plt.plot(x,y)

输出 [402]

[<matplotlib.lines.Line2D at 0x1eab9d3ee10>]

代码块 [403]

trainx, testx = x[0:int(0.8*(len(x)))], x[int(0.8*(len(x))):]
trainy, testy = y[0:int(0.8*(len(y)))], y[int(0.8*(len(y))):]
train = numpy.array(list(zip(trainx,trainy)))
test = numpy.array(list(zip(trainx,trainy)))

现在数据已经创建并被分成训练集和测试集。让我们根据回溯期的值将时间序列数据转换为监督学习数据的形式，这实际上是预测时间‘t’的值所看到的滞后数量。

因此，像这样的时间序列：

time variable_x
t1  x1
t2  x2
 :   :
 :   :
T   xT

当回溯期为 1 时，将转换为：

x1   x2
x2   x3
 :    :
 :    :
xT-1 xT

代码块 [404]

def create_dataset(n_X, look_back):
   dataX, dataY = [], []
   for i in range(len(n_X)-look_back):
      a = n_X[i:(i+look_back), ]
      dataX.append(a)
      dataY.append(n_X[i + look_back, ])
   return numpy.array(dataX), numpy.array(dataY)

代码块 [405]

look_back = 1
trainx,trainy = create_dataset(train, look_back)
testx,testy = create_dataset(test, look_back)

trainx = numpy.reshape(trainx, (trainx.shape[0], 1, 2))
testx = numpy.reshape(testx, (testx.shape[0], 1, 2))

现在我们将训练我们的模型。

将少量训练数据批次显示给网络，当整个训练数据以批次形式显示给模型并计算误差时的一次运行称为一个 epoch。 epochs 需要运行直到误差减少。

代码块 []

from keras.models import Sequential
from keras.layers import LSTM, Dense

model = Sequential()
model.add(LSTM(256, return_sequences = True, input_shape = (trainx.shape[1], 2)))
model.add(LSTM(128,input_shape = (trainx.shape[1], 2)))
model.add(Dense(2))
model.compile(loss = 'mean_squared_error', optimizer = 'adam')
model.fit(trainx, trainy, epochs = 2000, batch_size = 10, verbose = 2, shuffle = False)
model.save_weights('LSTMBasic1.h5')

代码块 [407]

model.load_weights('LSTMBasic1.h5')
predict = model.predict(testx)

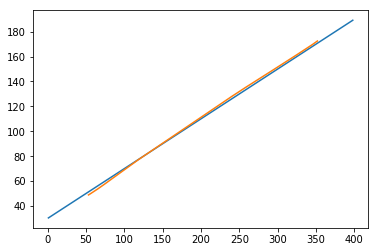
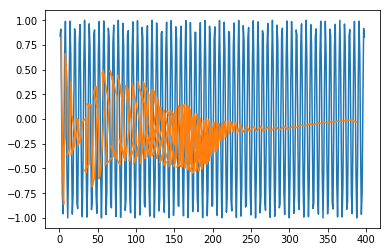
现在让我们看看我们的预测结果如何。

代码块 [408]

plt.plot(testx.reshape(398,2)[:,0:1], testx.reshape(398,2)[:,1:2])
plt.plot(predict[:,0:1], predict[:,1:2])

输出 [408]

[<matplotlib.lines.Line2D at 0x1eac792f048>]

现在，我们应该尝试以类似的方式对正弦或余弦波进行建模。您可以运行下面给出的代码并修改模型参数以查看结果如何变化。

代码块 [409]

x = numpy.arange (1,500,1)
y = numpy.sin(x)
plt.plot(x,y)

输出 [409]

[<matplotlib.lines.Line2D at 0x1eac7a0b3c8>]

代码块 [410]

trainx, testx = x[0:int(0.8*(len(x)))], x[int(0.8*(len(x))):]
trainy, testy = y[0:int(0.8*(len(y)))], y[int(0.8*(len(y))):]
train = numpy.array(list(zip(trainx,trainy)))
test = numpy.array(list(zip(trainx,trainy)))

代码块 [411]

look_back = 1
trainx,trainy = create_dataset(train, look_back)
testx,testy = create_dataset(test, look_back)
trainx = numpy.reshape(trainx, (trainx.shape[0], 1, 2))
testx = numpy.reshape(testx, (testx.shape[0], 1, 2))

代码块 []

model = Sequential()
model.add(LSTM(512, return_sequences = True, input_shape = (trainx.shape[1], 2)))
model.add(LSTM(256,input_shape = (trainx.shape[1], 2)))
model.add(Dense(2))
model.compile(loss = 'mean_squared_error', optimizer = 'adam')
model.fit(trainx, trainy, epochs = 2000, batch_size = 10, verbose = 2, shuffle = False)
model.save_weights('LSTMBasic2.h5')

代码块 [413]

model.load_weights('LSTMBasic2.h5')
predict = model.predict(testx)

代码块 [415]

plt.plot(trainx.reshape(398,2)[:,0:1], trainx.reshape(398,2)[:,1:2])
plt.plot(predict[:,0:1], predict[:,1:2])

输出 [415]

[<matplotlib.lines.Line2D at 0x1eac7a1f550>]

现在您可以开始处理任何数据集了。

时间序列 - 误差指标

量化模型的性能以将其用作反馈和比较非常重要。在本教程中，我们使用了最流行的误差指标之一：均方根误差。还有其他各种可用的误差指标。本章简要讨论了这些指标。

均方误差

它是预测值和真实值之间差值的平方平均值。Sklearn 提供它作为函数。它具有与真实值和预测值的平方相同的单位，并且始终为正。

$$MSE = \frac{1}{n} \displaystyle\sum\limits_{t=1}^n \lgroup y'_{t}\:-y_{t}\rgroup^{2}$$

其中 $y'_{t}$ 是预测值，

$y_{t}$ 是实际值，并且

n 是测试集中值的总数。

从方程中可以清楚地看出，MSE 对较大的误差或异常值惩罚更大。

均方根误差

它是均方误差的平方根。它也始终为正，并且在数据的范围内。

$$RMSE = \sqrt{\frac{1}{n} \displaystyle\sum\limits_{t=1}^n \lgroup y'_{t}-y_{t}\rgroup ^2}$$

其中，$y'_{t}$ 是预测值

$y_{t}$ 是实际值，并且

n 是测试集中值的总数。

它是一次方的，因此与 MSE 相比更易于解释。RMSE 对较大误差的惩罚也更大。我们在教程中使用了 RMSE 指标。

平均绝对误差

它是预测值和真实值之间绝对差值的平均值。它与预测值和真实值的单位相同，并且始终为正。

$$MAE = \frac{1}{n}\displaystyle\sum\limits_{t=1}^{t=n} | y'{t}-y_{t}\lvert$$

其中，$y'_{t}$ 是预测值，

$y_{t}$ 是实际值，并且

n 是测试集中值的总数。

平均百分比误差

它是预测值和真实值之间绝对差值的平均值百分比，除以真实值。

$$MAPE = \frac{1}{n}\displaystyle\sum\limits_{t=1}^n\frac{y'_{t}-y_{t}}{y_{t}}*100\: \%$$

其中，$y'_{t}$ 是预测值，

$y_{t}$ 是实际值，n 是测试集中值的总数。

但是，使用此误差的缺点是正误差和负误差可以相互抵消。因此，使用平均绝对百分比误差。

平均绝对百分比误差

它是预测值和真实值之间绝对差值的平均值百分比，除以真实值。

$$MAPE = \frac{1}{n}\displaystyle\sum\limits_{t=1}^n\frac{|y'_{t}-y_{t}\lvert}{y_{t}}*100\: \%$$

其中 $y'_{t}$ 是预测值

$y_{t}$ 是实际值，并且

n 是测试集中值的总数。

时间序列 - 应用

在本教程中，我们讨论了时间序列分析，这使我们了解到时间序列模型首先从现有的观测中识别趋势和季节性，然后根据这种趋势和季节性预测值。这种分析在各个领域都很有用，例如：

财务分析——包括销售预测、库存分析、股票市场分析、价格估算。
天气分析——包括温度估算、气候变化、季节性变化识别、天气预报。
网络数据分析——包括网络使用预测、异常或入侵检测、预测性维护。
医疗保健分析——包括人口普查预测、保险福利预测、病人监控。

时间序列 - 进一步研究

机器学习处理各种类型的问题。事实上，几乎所有领域都有可能借助机器学习实现自动化或改进。下面列出了一些正在进行大量工作的此类问题。

时间序列数据

这是根据时间变化的数据，因此时间在其中起着至关重要的作用，我们在本教程中对此进行了广泛的讨论。

非时间序列数据

它是不依赖于时间的数据，大部分机器学习问题都集中在非时间序列数据上。为简单起见，我们将对其进行进一步分类：

数值数据 − 与人类不同，计算机只理解数字，因此所有类型的数据最终都会被转换为数值数据用于机器学习，例如，图像数据被转换为 (r,b,g) 值，字符被转换为 ASCII 码或单词被索引为数字，语音数据被转换为包含数值数据的 mfcc 文件。
图像数据 − 计算机视觉彻底改变了计算机的世界，它在医学、卫星成像等领域有着广泛的应用。
文本数据 − 自然语言处理 (NLP) 用于文本分类、释义检测和语言摘要。这就是让谷歌和Facebook变得智能的原因。
语音数据 − 语音处理涉及语音识别和情感理解。它在赋予计算机类人品质方面发挥着至关重要的作用。

打印页面