时间序列 - 自回归

对于平稳时间序列，自回归模型将时间 't' 处的变量值视为其之前 'p' 个时间步长的值的线性函数。数学上可以写成 -

$$y_{t} = \:C+\:\phi_{1}y_{t-1}\:+\:\phi_{2}Y_{t-2}+...+\phi_{p}y_{t-p}+\epsilon_{t}$$

其中，‘p’ 是自回归趋势参数

$\epsilon_{t}$ 是白噪声，并且

$y_{t-1}, y_{t-2}\:\: ...y_{t-p}$ 表示变量在先前时间段的值。

可以使用各种方法校准 p 的值。找到 'p' 的合适值的一种方法是绘制自相关图。

注意 - 在对数据进行任何分析之前，我们应该将数据以 8:2 的比例分成训练集和测试集，因为测试数据仅用于找出模型的准确性，并且假设是，在进行预测之前，我们无法获得它。在时间序列的情况下，数据点的顺序非常重要，因此在分割数据时应注意不要丢失顺序。

自相关图或相关图显示了变量与其自身在先前时间步长的关系。它利用皮尔逊相关系数，并在 95% 的置信区间内显示相关性。让我们看看它在我们数据的“温度”变量中是什么样的。

显示 ACP

在 [141]

split = len(df) - int(0.2*len(df))
train, test = df['T'][0:split], df['T'][split:]

在 [142]

from statsmodels.graphics.tsaplots import plot_acf

plot_acf(train, lags = 100)
plt.show()

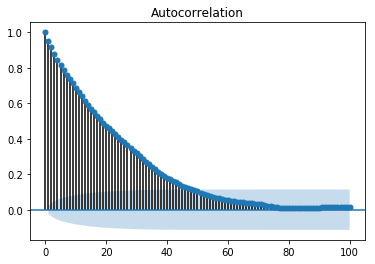
所有位于阴影蓝色区域之外的滞后值都被认为具有相关性。