
时间序列 - ARIMA 的变体
在上一章中,我们已经了解了 ARIMA 模型的工作原理及其局限性,即它无法处理季节性数据或多元时间序列,因此,引入了新的模型来包含这些特征。
以下是这些新模型的简要介绍:
向量自回归 (VAR)
它是多元平稳时间序列的自回归模型的推广版本。其特征在于参数 'p'。
向量移动平均 (VMA)
它是多元平稳时间序列的移动平均模型的推广版本。其特征在于参数 'q'。
向量自回归移动平均 (VARMA)
它是 VAR 和 VMA 的组合,也是多元平稳时间序列的 ARMA 模型的推广版本。其特征在于参数 'p' 和 'q'。就像 ARMA 通过将参数 'q' 设置为 0 可以充当 AR 模型,通过将参数 'p' 设置为 0 可以充当 MA 模型一样,VARMA 也能够通过将参数 'q' 设置为 0 充当 VAR 模型,通过将参数 'p' 设置为 0 充当 VMA 模型。
代码块 [209]
df_multi = df[['T', 'C6H6(GT)']] split = len(df) - int(0.2*len(df)) train_multi, test_multi = df_multi[0:split], df_multi[split:]
代码块 [211]
from statsmodels.tsa.statespace.varmax import VARMAX model = VARMAX(train_multi, order = (2,1)) model_fit = model.fit() c:\users\naveksha\appdata\local\programs\python\python37\lib\site-packages\statsmodels\tsa\statespace\varmax.py:152: EstimationWarning: Estimation of VARMA(p,q) models is not generically robust, due especially to identification issues. EstimationWarning) c:\users\naveksha\appdata\local\programs\python\python37\lib\site-packages\statsmodels\tsa\base\tsa_model.py:171: ValueWarning: No frequency information was provided, so inferred frequency H will be used. % freq, ValueWarning) c:\users\naveksha\appdata\local\programs\python\python37\lib\site-packages\statsmodels\base\model.py:508: ConvergenceWarning: Maximum Likelihood optimization failed to converge. Check mle_retvals "Check mle_retvals", ConvergenceWarning)
代码块 [213]
predictions_multi = model_fit.forecast( steps=len(test_multi)) c:\users\naveksha\appdata\local\programs\python\python37\lib\site-packages\statsmodels\tsa\base\tsa_model.py:320: FutureWarning: Creating a DatetimeIndex by passing range endpoints is deprecated. Use `pandas.date_range` instead. freq = base_index.freq) c:\users\naveksha\appdata\local\programs\python\python37\lib\site-packages\statsmodels\tsa\statespace\varmax.py:152: EstimationWarning: Estimation of VARMA(p,q) models is not generically robust, due especially to identification issues. EstimationWarning)
代码块 [231]
plt.plot(train_multi['T']) plt.plot(test_multi['T']) plt.plot(predictions_multi.iloc[:,0:1], '--') plt.show() plt.plot(train_multi['C6H6(GT)']) plt.plot(test_multi['C6H6(GT)']) plt.plot(predictions_multi.iloc[:,1:2], '--') plt.show()
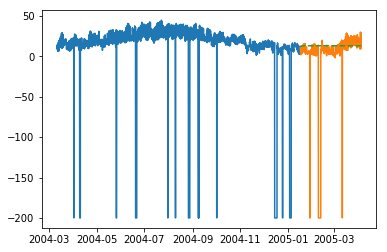
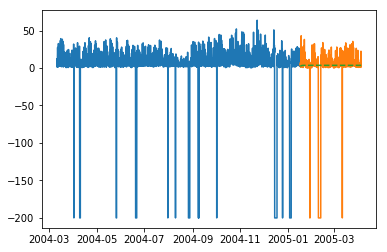
上述代码展示了如何使用 VARMA 模型对多元时间序列进行建模,尽管此模型可能并不最适合我们的数据。
带有外生变量的 VARMA (VARMAX)
它是 VARMA 模型的扩展,其中使用称为协变量的额外变量来对我们感兴趣的主要变量进行建模。
季节性自回归积分移动平均 (SARIMA)
这是 ARIMA 模型的扩展,用于处理季节性数据。它将数据划分为季节性和非季节性成分,并以类似的方式对它们进行建模。它具有 7 个参数,非季节性部分的参数 (p,d,q) 与 ARIMA 模型相同,季节性部分的参数为 (P,D,Q,m),其中 'm' 是季节周期数,P、D、Q 与 ARIMA 模型的参数类似。这些参数可以使用网格搜索或遗传算法进行校准。
带有外生变量的 SARIMA (SARIMAX)
这是 SARIMA 模型的扩展,其中包含有助于我们对感兴趣变量进行建模的外生变量。
在将变量作为外生变量之前,进行变量的相关性分析可能会有所帮助。
代码块 [251]
from scipy.stats.stats import pearsonr
x = train_multi['T'].values
y = train_multi['C6H6(GT)'].values
corr , p = pearsonr(x,y)
print ('Corelation Coefficient =', corr,'\nP-Value =',p)
Corelation Coefficient = 0.9701173437269858
P-Value = 0.0
皮尔逊相关系数显示了两个变量之间的线性关系,为了解释结果,我们首先查看 p 值,如果它小于 0.05,则系数的值是显著的,否则系数的值不显著。对于显著的 p 值,正的相关系数值表示正相关,负的相关系数值表示负相关。
因此,对于我们的数据,“温度”和“C6H6”似乎具有高度正相关。因此,我们将
代码块 [297]
from statsmodels.tsa.statespace.sarimax import SARIMAX model = SARIMAX(x, exog = y, order = (2, 0, 2), seasonal_order = (2, 0, 1, 1), enforce_stationarity=False, enforce_invertibility = False) model_fit = model.fit(disp = False) c:\users\naveksha\appdata\local\programs\python\python37\lib\site-packages\statsmodels\base\model.py:508: ConvergenceWarning: Maximum Likelihood optimization failed to converge. Check mle_retvals "Check mle_retvals", ConvergenceWarning)
代码块 [298]
y_ = test_multi['C6H6(GT)'].values predicted = model_fit.predict(exog=y_) test_multi_ = pandas.DataFrame(test) test_multi_['predictions'] = predicted[0:1871]
代码块 [299]
plt.plot(train_multi['T']) plt.plot(test_multi_['T']) plt.plot(test_multi_.predictions, '--')
输出 [299]
[<matplotlib.lines.Line2D at 0x1eab0191c18>]
与单变量 ARIMA 建模相比,这里的预测似乎现在出现了更大的变化。
毋庸置疑的是,SARIMAX 可以通过仅将相应参数设置为非零值来用作 ARX、MAX、ARMAX 或 ARIMAX 模型。
分数自回归积分移动平均 (FARIMA)
有时,我们的序列可能不是平稳的,而使用参数 'd' 取值 1 进行差分可能会过度差分。因此,我们需要使用分数值对时间序列进行差分。
在数据科学领域,没有一个最优模型,适用于您的数据的模型在很大程度上取决于您的数据集。了解各种模型使我们能够选择一个适用于我们数据的模型,并通过实验获得最佳结果。结果应该以图表和误差指标的形式呈现,有时即使是小的误差也可能是坏的,因此,绘制和可视化结果至关重要。
在下一章中,我们将研究另一个统计模型:指数平滑。