平行四边形的角

---

介绍

平行四边形的内角和为 360 度。平行四边形有四个内角，这些内角的总和始终为 360°。在平行四边形中，邻角互补，对角相等。让我们更详细地了解平行四边形角的特征。以下是几何图形平行四边形 IJKL，其中 $\mathrm{IJ\:=\:LK\:}$ & $\mathrm{JK\:=\:IL}$

$$\mathrm{IJ\:\rVert\:LK\:\:,\:JK\rVert\:IL}$$

也就是说，对边相等且平行，对角线互相平分，它们在点 O 处相交。在平行四边形中，对角的度数相同，即 $\mathrm{\angle\:I=\:\angle\:k}$ & $\mathrm{\angle\:J\:=\:\angle\:L}$

平行四边形

平行四边形是一种四边形，其一对对边长度相等，对角的度数相等。

平行四边形的性质

• 平行四边形是四边形

• 它是一个有 4 条边和 4 个角的多边形

• 在平行四边形中，对边长度相等

• 在平行四边形中，对角的度数相等

• 在平行四边形中，对角线不相等

• 在平行四边形中，对角线在公共点处相交，并在交点处互相平分

• 在平行四边形中，有两对对边平行

• 在平行四边形中，可以应用内错角定理和同位角定理

涉及角的性质

• 在平行四边形中，对角相等（或全等）

• 连续角互补（即它们加起来等于 180 度）

• 平行四边形的对角相等。

• 上述定理的逆定理指出，如果四边形的对角相等，则该四边形是平行四边形。

• 平行四边形的任何连续角都是互补的。

• 平行四边形的两个相邻角加起来等于 180°。

• 如果平行四边形中的一个角是直角，则所有四个角都是直角

涉及边的性质

• 在平行四边形中，对边全等

• 平行四边形的对角线互相平分。

• 平行四边形的每条对角线将其分成两个全等三角形。

例题

1)如果平行四边形中两个相邻角分别为 $\mathrm{x°}$ & $\mathrm{2x°}$，则求平行四边形中每个角的度数。

解答 - 在平行四边形中，对角的度数相等。

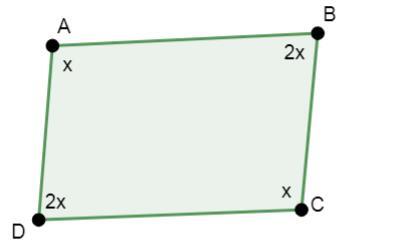
在上图中，角 A 和角 B 分别为 $\mathrm{x°}$ & $\mathrm{2x°}$。

利用四边形的内角和性质，我们得到：

$$\mathrm{x\:+\:2x\:x\:+\:2x\:=\:360}$$

$$\mathrm{6x\:=\:360}$$

$$\mathrm{x\:=\:60}$$

因此，每个角的度数分别为 60°、120°、60° 和 120°

2)求下图中未知角的度数。

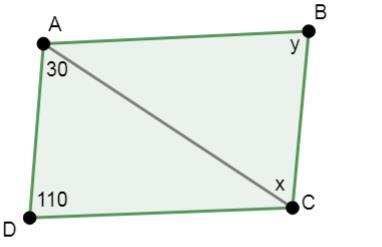
解答 -

在平行四边形 ABCD 中，$\mathrm{AB\:\rvert\:DC\:and\:AC}$ 是它的横截线。

因此，内错角的度数相等。

$$\mathrm{\angle\:DAC\:=\:\angle\:ACB\:\Longrightarrow\:x\:=\:30°}$$

在平行四边形中，对角的度数相等。

因此，

$$\mathrm{\angle\:ADC\:=\:angle\:ABC\:\Longrightarrow\:y\:=\:110°}$$

3)确定以下平行四边形中未知边的长度。

解答 - 在平行四边形中，对边的长度相同。

因此，

$$\mathrm{x\:=\:6\:\&\:y\:=\:12}$$

因此，未知边的长度分别为 6 和 12 个单位。

4)如果平行四边形中两个相邻角分别为 $\mathrm{2x°\:\&\:4x°}$，则求平行四边形中每个角的度数。

解答 - 在平行四边形中，对角的度数相等。

利用四边形的内角和性质，我们得到：

$$\mathrm{2x\:+\:4x\:+\:2x\:+\:4x\:=360}$$

$$\mathrm{12x\:=\:360}$$

$$\mathrm{x\:=\:30}$$

5)确定以下平行四边形 IJKL 中角 𝒚 的度数

解答 -

我们知道，平行四边形中的对角的度数相等。因此，

$$\mathrm{\angle\:I\:=\:\angle\:K\:=\:110°\:\&\:\angle\:J\:=\:\angle\:L\:=\:x}$$

由于四边形四个角的和为 360 度，因此

$$\mathrm{\angle\:I\:+\:\angle\:J\:+\:\angle\:K\:+\:\angle\:L\:=\:360°}$$

$$\mathrm{110\:+\:x\:+\:110\:+\:x\:=\:360°}$$

$$\mathrm{2x\:+\:220\:=\:360°}$$

$$\mathrm{2x\:=\:140}$$

$$\mathrm{x\:=\:70}$$

6)平行四边形涉及角的最重要的性质是什么？

解答 - 以下是由平行四边形涉及角的最重要的性质：

• 平行四边形的对角相等（或全等）

• 以下角互补（即它们加起来等于 180 度）

• 平行四边形的对角线有相等的角。

• 上述定理的逆定理指出，如果四边形的对边上的角相等，则它是一个平行四边形。

• 平行四边形的任何连续角都是互补的。

• 平行四边形的两个相邻角之和为 180°。

• 如果平行四边形中的四个角之一是直角，则所有四个角都是直角。

结论

根据以上关于平行四边形的讨论，我们可以得出以下关于平行四边形的结论：

• 如果平行四边形的边完全相等，则该形状称为菱形。

• 菱形也可以使用平行四边形的性质。

• 如果平行四边形中的一对边平行，则该形状称为梯形。

• 平行边和非平行边分别称为底和腰。

• 如果腰全等，则我们有等腰梯形。

常见问题

1. 什么使平行四边形中的角独一无二？

对角排成一行。如果任何一个角是直角，则所有角都将是直角。两条对角线互相穿过。

2. 哪个/哪些平行四边形的角是连续角？

平行四边形的相邻角通常被称为连续角，并且始终互补（180°）。

3. 哪个平行四边形的角相等？

平行四边形的内角必须相等且相对。四个内角的总和也必须等于 180 度。周围的内角也必须互补（度数之和）。由于它们彼此相邻，因此角度必须是互补角。

4. 为什么平行四边形中的对角相等？

由于对边的长度相同，因此两条对角线上的正方形相同。已经证明，对角线互相平分的四边形是平行四边形。由于 ABCD 是平行四边形，因此它的对边长度相同。(全等三角形的对应角)。

5. 平行四边形的重要性质是什么？

顾名思义，平行四边形是一个简单的四边形，其对边平行。因此，有两组平行边。平行四边形还有相等的对角和互相平分的对角线。

6. 四边形的四条边长度是否相等？

存在正四边形和不规则四边形。正四边形必须有四条相等的边、四个相等的角和互相平分的对角线。唯一满足所有这些条件的四边形是正方形。

7. 平行四边形中可以有两个直角吗？

具有两组平行边的四边形称为平行四边形。这些图形的边彼此平行且颜色相同。具有四个等长边的形状。该形状没有直角，并且有两组平行边。