坐标轴与已知直线形成的三角形面积?
这里我们将学习如何求由x轴、y轴和另一条直线围成的三角形的面积。图形如下所示。直线的方程为:
𝑎𝑥+𝑏𝑦+𝑐=0

该直线与x轴相交于点B,与y轴相交于点A。截距式方程如下:
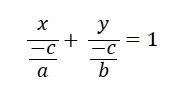
因此,x截距为−𝑐∕𝑎,y截距为−𝑐∕𝑏。所以三角形的面积是
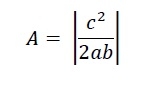
示例
在线演示
#include<iostream>
#include<cmath>
using namespace std;
double areaTriangle(double a, double b, double c){
return fabs((c*c) / (2*a*b));
}
main() {
double a = -2, b = 4, c = 3;
cout << "Area: " << areaTriangle(a, b, c);
}输出
Area: 0.5625
- 相关文章
- 绘制方程$\frac{x}{3} + \frac{y}{4} = 1$的图像。并求出该直线与坐标轴围成的三角形的面积。
- 绘制方程$5x\ -\ y\ =\ 5$和$3x\ -\ y\ =\ 3$的图像。确定由这两条直线和y轴围成的三角形的顶点坐标。计算该三角形的面积。
- 在同一张图纸上绘制下列线性方程的图像。$2x + 3y = 12, x -y = 1$找到由两条直线和y轴围成的三角形的顶点坐标。并求出三角形的面积。
- 求顶点为$(0, -1), (2, 1)$和$(0, 3)$的三角形各边中点连线形成的三角形的面积。求此三角形面积与原三角形面积的比值。
- 解释三角学中的坐标。
- 用C++表示给定的一组点,使其尽可能拟合一条直线。
- 求直线$x+y=10$与坐标轴围成的面积。
- 求线段$(-2, -3)$和$(5, 6)$被x轴分割的比例。并求出分割点的坐标。
- 求线段$(-2, -3)$和$(5, 6)$被y轴分割的比例。并求出分割点的坐标。
- $ABC$是一个三角形,直线$PQ$交$AB$于$P$点,交$AC$于$Q$点。如果$AP = 1\ cm, PB = 3\ cm, AQ = 1.5\ cm, QC = 4.5\ cm$,证明$\triangle APQ$的面积是$\triangle ABC$面积的十六分之一。
- 点P的坐标为$(-3,2)$。求在连接P点和原点的直线上,且满足$OP = OQ$的点Q的坐标。
- 用C++求给定底边和面积的三角形的最小高度。
- 解释三角形的周长和面积。
- 求$a$的值,使得由点$A (a, 2a), B (-2, 6)$和$C (3, 1)$组成的三角形的面积为10平方单位。
- 直线法计算折旧

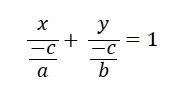
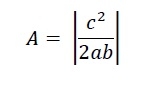


 数据结构
数据结构 网络
网络 关系数据库管理系统(RDBMS)
关系数据库管理系统(RDBMS) 操作系统
操作系统 Java
Java iOS
iOS HTML
HTML CSS
CSS Android
Android Python
Python C语言编程
C语言编程 C++
C++ C#
C# MongoDB
MongoDB MySQL
MySQL Javascript
Javascript PHP
PHP