数据结构
网络
关系数据库管理系统
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 语言编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理学
化学
生物学
数学
英语
经济学
心理学
社会学
服装设计
法律研究
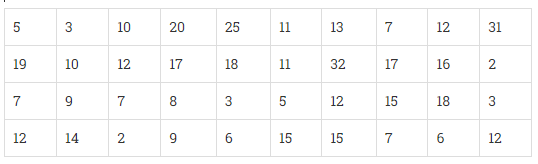
已知：40 名工程师从住所到工作地点的距离（单位：公里）
已知：三角形 ABC 的角 A、B 和 C 的角平分线分别与它的外接圆交于 D、E 和 F。
已知：AC 和 BD 是一个圆的弦，它们互相平分。
需要做：我们需要证明以菱形任意一边为直径的圆经过其对角线的交点。
已知：ABCD 是一个平行四边形。过 A、B 和 C 的圆与 CD（必要时延长）交于 E。
已知：一个圆的两个弦 AB 和 CD 的长度分别为 5 厘米和 11 厘米，它们互相平行且位于圆心的两侧。
已知：一个圆的两个平行弦的长度分别为 6 厘米和 8 厘米。
已知：设角\( \mathrm{ABC} \)的顶点位于圆外，且角的两边与圆相交于相等的弦\( \mathrm{AD} \)和\( \mathrm{CE} \)。求证：\( \angle \mathrm{ABC} \)等于弦\( AC \)和\( DE \)在圆心处所对的角之差的一半。证明：$AD = CE$我们知道，三角形的外角等于两个内对角的和。这意味着，在$\triangle BAE$中，$\angle DAE = \angle ABC+\angle AEC$........(i)$DE$在圆心处所对的角为$\angle DOE$ ... 阅读更多
求证：两个相交圆的连心线在两个交点处所对的角相等。证明：设两个圆心分别为$A$和$A'$，且这两个圆相交于$B$和$B'$。在$\triangle BAA’$和$\triangle B'AA’$中$AB = AB'$ (圆心为$A$的圆的半径)$A’B = A’B'$ (圆心为$A'$的圆的半径)$AA’ = AA’$ (公共边)因此，根据$SSS$全等，$\triangle BAA’ \cong \triangle B'AA’$这意味着，$\angle ABA' = \angle AB'A’$综上所述，两个相交圆的连心线在两个交点处所对的角... 阅读更多
已知：\( \mathrm{ABC} \)和\( \mathrm{ADC} \)是两个以\( \mathrm{AC} \)为公共斜边的直角三角形。求证：\( \angle \mathrm{CAD}=\angle \mathrm{CBD} \)。证明：我们知道，同弧所对的圆周角相等。这意味着，$\angle CBD=\angle CAD$证毕。