数据结构
网络
关系数据库管理系统 (RDBMS)
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 语言编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理学
化学
生物学
数学
英语
经济学
心理学
社会学
服装学
法学
已知：以三角形的两条边为直径作圆。 求证：这两个圆的交点位于第三条边上。证明：设三角形为PQR，两个圆的直径分别为PQ和PR。我们知道，半圆中的角是直角。这意味着，∠PSQ = ∠PSR = 90° ∠PSQ+∠PSR = 180° 因此，∠BDC是一条直线。所以，我们可以说S位于QR线上。 证毕。
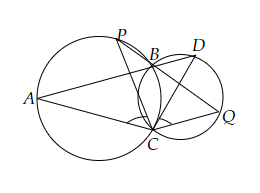
"\已知：两圆相交于两点\( B \)和\( C \)。过\( \mathrm{B} \)，作两条线段\( \mathrm{ABD} \)和\( \mathrm{PBQ} \)分别与圆相交于\( A, D \)和\( P \), \( Q \)。求证：\( \angle \mathrm{ACP}=\angle \mathrm{QCD} \)。证明：我们知道，同弧所对的圆周角相等。在较大的圆中，∠ACP =∠ABP……(i) (同弧所对的圆周角)在较小的圆中，∠QCD = ∠QBD……(ii) (同弧所对的圆周角)∠ABP = ... 阅读更多
已知：梯形的两条非平行边相等。求证：它是圆内接四边形。证明：设梯形为PQRS，其中PQ∥RS且PS=QR。作PM⊥RS和QN⊥RS。在△PSM和△QRN中，PS=QR，∠PMS=∠QNR=90°，PM=QN (两平行线间的垂直距离相等)。因此，根据RHS全等，△PMS≅QNR。这意味着，∠PSR=∠QRS……(i) (全等三角形对应角相等)∠QPS和∠PSR在横截线PS的同侧，∠QPS+∠PSR=180°，∠QPS+∠QRS=180° [由(i)]这意味着，对角互补。因此，所给梯形是圆内接四边形。阅读更多
已知：圆内接四边形的对角线是过四边形顶点的圆的直径。求证：它是矩形。证明：设PR和QS是圆内接四边形PQRS的对角线。这意味着，PR和QS是圆的直径。PR=QS，OP=OQ=OR=OS (圆的半径)四边形PQRS的对角线相等且互相平分。因此，四边形PQRS是矩形。证毕。
已知：\( \mathrm{ABCD} \)是一个圆内接四边形，其对角线相交于点\( \mathrm{E} \)。 \( \angle \mathrm{DBC}=70^{\circ} \)， \( \angle \mathrm{BAC} \)是\( 30^{\circ} \)，\( \mathrm{AB}=\mathrm{BC} \)。求\( \angle \mathrm{BCD} \)和\( \angle \mathrm{ECD} \)。解：我们知道，同弧所对的圆周角相等。这意味着，∠BDC = ∠BAC=30°在△BCD中，∠BDC + ∠DBC + ∠BCD = 180° 30°+70°+∠BCD=180° 100°+∠BCD=180° ∠BCD=180°-100° ∠BCD=80° AB = BC，这意味着∠BCA = ∠BAC= 30° (等边对等角)∠ ... 阅读更多
已知：球的直径减少了\( 25 \% \)。求：表面积减少的百分比。解：设球的初始直径为d。这意味着，球的初始半径r=d/2。球的初始表面积 = 4π(d/2)² = 4πd²/4 = πd²。直径减少25%后，新的直径d₁=d-25d/100 = 75d/100 = 3d/4。新球的表面积 = 4π(d₁/2)² = 4π(1/2×3d/4)² = 4π(9d²/64) = 9πd²/16。球的表面积减少量 = πd²(1-9/16) = πd²(7/16)。因此，表面积减少的百分比 = ... 阅读更多
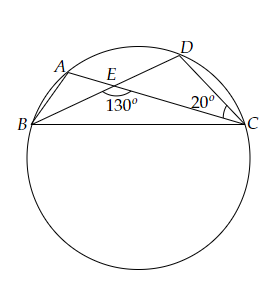
"\已知：A、B、C和D是圆上的四个点。\( \mathrm{AC} \)和\( \mathrm{BD} \)相交于点\( \mathrm{E} \)，使得\( \angle \mathrm{BEC}=130^{\circ} \)和\( \angle \mathrm{ECD}=20^{\circ} \)。求\( \angle \mathrm{BAC} \)。解：我们知道，同弧所对的圆周角相等。这意味着，∠BAC = ∠CDE，∠CEB = ∠CDE+∠ECD (外角性质) 130°=∠CDE+20° ∠CDE=130°-20° =110° 因此，∠BAC=∠CDE=110°。所以，∠BAC = 110°。
已知：一堆小麦呈圆锥形，直径为\( 10.5 \mathrm{~m} \)，高度为\( 3 \mathrm{~m} \)。求：求其体积和覆盖这堆小麦所需的帆布面积。解：小麦圆锥形堆的直径 = 10.5 m这意味着，半径 (r) = \(\frac{10.5}{2} \mathrm{~m}\) = 5.25 m圆锥形堆的高度 (h) = 3 m堆的体积 = \(\frac{1}{3} \pi r^{2} h\) = \(\frac{1}{3} \times \frac{22}{7} \times 5.25 \times 5.25 \times 3\) = 86.625 m³我们知道，\(l^2=r^2+h^2\) \(\Rightarrow l=\sqrt{r^{2}+h^{2}}\) = \(\sqrt{(5.25)^{2}+(3)^2}\) = \(\sqrt{27.5625+9}\) = \(\sqrt{36.5625}\) = 6.05堆的侧面积 = πrl = \(\frac{22}{7}\) × 5.25 × 6.05 = 99.825 cm²所需的帆布面积为 99.825 cm²。阅读更多
已知：球体的半径为 (i) \( 7 \mathrm{~cm} \) (ii) \( 0.63 \mathrm{~m} \)。求：求出两种情况下球体的体积。解：我们知道，半径为 r 的球体的体积为 \(\frac{4}{3} \pi r^3\)因此，(i) 半径为 7 cm 的球体的体积 = \(\frac{4}{3} \pi (7)^3\) = \(\frac{4}{3} \times \frac{22}{7} \times (7)^3\) = \(\frac{4312}{3}\) cm³因此，球体的体积为 \(\frac{4312}{3}\) cm³ (ii) 半径为 0.63 m 的球体的体积 = \(\frac{4}{3} \pi (0.63)^3\) = \(\frac{4}{3} \times \frac{22}{7} \times (0.63)^3\) = \(88 \times 0.3969 \times 0.03\) = 1.0478 m³ ≈ 1.05 m³因此，球体的体积为 1.05 m³。
已知：实心球形球的直径为 (i) \( 28 \mathrm{~cm} \) (ii) \( 0.21 \mathrm{~m} \)。求：求出两种情况下实心球形球所排开的少量水。解：(i) 实心球形球的直径 = 28 cm实心球形球的半径 r = \(\frac{28}{2}\) cm = 14 cm实心球形球所排开的水 = 实心球形球的体积 = \(\frac{4}{3} \pi r^{3}\) = \(\frac{4}{3} \times \frac{22}{7} \times(14)^{3}\) = \(\frac{4}{3} \times \frac{22}{7} \times 14 \times 14 \times 14\) = 11498.66 cm³ (ii) 实心球形球的直径 = 0.21 m实心球形球的半径 r = \(\frac{0.21}{2}\) m = 0.105 m实心球形球所排开的水...阅读更多