数据结构
网络
关系型数据库管理系统
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 语言编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理学
化学
生物学
数学
英语
经济学
心理学
社会学
服装设计
法律研究
给定：一个公交车站被用 $50$ 个由再生纸板制成的空心圆锥体与道路的其余部分隔开。每个圆锥体的底座直径为 $40\ cm$，高度为 $1\ m$。每个圆锥体的外部都需要喷漆，喷漆成本为每平方米 $Rs.\ 12$。要求：我们需要计算喷漆这些圆锥体的成本。 解答：圆锥体底座的直径 $= 40\ cm$这意味着，圆锥体底座的半径 $(r) = \frac{40}{2}$$=20 \mathrm{~cm}$$=0.2 \mathrm{~m}$圆锥体的高度 $(h)=1 \mathrm{~m}$$=100 \mathrm{~cm}$因此，圆锥体的斜高 $(l)=\sqrt{r^{2}+h^{2}}$$=\sqrt{(20)^{2}+(100)^{2}}$$=\sqrt{400+10000}$$=\sqrt{10400} ... 阅读更多
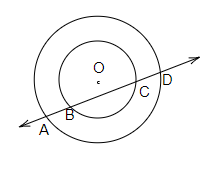
"\给定：$A,B$ 和 $C$ 是一个圆上的三个点，圆心为 $O$，使得 $\angle BOC = 30^o$ 且 $\angle AOB = 60^o$。$D$ 是圆上除弧 $ABC$ 外的任意一点。要求：我们需要求 $\angle ADC$。解答：$\angle AOC = \angle AOB+\angle BOC$$\angle AOC = 60^o+30^o$$\angle AOC = 90^o$我们知道，圆周角等于圆心角的一半。因此，$\angle ADC = \frac{1}{2}\angle AOC$$= \frac{1}{2}\times 90^o$$= 45^o$因此，$\angle ADC =45^o$。
"\给定：$\angle PQR = 100^o$，其中 $P, Q$ 和 $R$ 是一个圆上的三个点，圆心为 $O$。要求：我们需要求 $\angle OPR$。解答：我们知道，圆周角等于圆心角的一半。这意味着，$\angle POR$ 的圆心角 $= 2\angle PQR$$\angle POR$ 的圆心角 $= 2\times100^o$$= 200^o$因此，$\angle POR = 360^o-200^o$$= 160^o$在 $\triangle OPR$ 中，$OP$ 和 $OR$ 是圆的半径。$OP = OR$这意味着，$\angle OPR = \angle ORP$$\angle POR+\angle OPR+\angle ORP = 180^o$$\angle OPR+\angle OPR = 180^o-160^o$$2\angle OPR = 20^o$$\angle OPR=\frac{20^o}{2}$$\angle OPR=10^o$因此， ... 阅读更多
"\给定：$\angle ABC = 69^o, \angle ACB = 31^o$要求：我们需要求 $\angle BDC$。解答：我们知道，同弧所对的圆周角相等。这意味着，$\angle BAC = \angle BDC$在 $\triangle ABC$ 中，$\angle ABC+\angle BAC+\angle ACB = 180^o$ (三角形的内角和为 $180^o$)$69^o+\angle BAC+31^o=180^o$$\angle BAC = 180^o-100^o$$\angle BAC = 80^o$这意味着，$\angle BAC=\angle BDC = 80^o$因此，$\angle BDC = 80^o$。
"\给定： 三个女孩瑞诗玛、萨尔玛和曼迪普在公园里一个半径为 \( 5 \mathrm{~m} \) 的圆上玩游戏。瑞诗玛把球扔给萨尔玛，萨尔玛扔给曼迪普，曼迪普扔给瑞诗玛。瑞诗玛和萨尔玛之间的距离以及萨尔玛和曼迪普之间的距离都为 \( 6 \mathrm{~m} \)。要求：我们需要求瑞诗玛和曼迪普之间的距离。解答：设 $R, S$ 和 $M$ 分别表示瑞诗玛、萨尔玛和曼迪普的位置。作垂线 $OA$ 和 $OB$ 分别垂直于 $RS$ 和 $SM$。$AR=AS= \frac{6}{2} =3\ m$$OR=OS=OM=5\ m$ [圆的半径]在 $\triangle OAR$$OA^2 + AR^2 = ... 阅读更多
给定：一个半径为 \( 20 \mathrm{~m} \) 的圆形公园位于一个小区内。三个男孩安库尔、赛义德和大卫等距地坐在公园的边界上，每个人都拿着一个玩具电话互相交谈。要求：我们需要求每个电话线的长度。解答：圆形公园的半径 $= 20\ m$安库尔、赛义德和大卫等距地坐着。连接这些点，形成一个等边三角形 $ABC$。延长 $BO$ 到 $L$，它是 $AC$ 的垂直平分线。因此，$BL = 20 + 10$$= 30\ m$ ... 阅读更多
给定：两个圆相交于两点要求：我们需要证明它们的圆心位于公共弦的垂直平分线上。解答：设两个圆心分别为 $O$ 和 $O'$，它们相交于 $A$ 和 $B$ 两点。$OA = OB$ (圆的半径)$O’A = O'B$ (圆的半径)$OO’ = OO’$ (公共边)因此，根据 SSS 全等，$\triangle AOO’$ 和 $\triangle BOO’$ 相似。这意味着，$\triangle AOO’ \cong \triangle BOO’$$\angle AOO’ = \angle BOO’$............(i)在 $\triangle AOC$ 和 \triangle BOC$ 中，$OA = OB$ ... 阅读更多
给定：两个圆的半径分别为 \( 5 \mathrm{~cm} \) 和 \( 3 \mathrm{~cm} \)。两个圆的圆心之间的距离为 \( 4 \mathrm{~cm} \)。要求：我们需要求公共弦的长度。解答： 在上图中，$AO=5\ cm, BO=3\ cm$$AB = 4\ cm, AC = x, BC = 4-x$。$OD$ 是两个圆的公共弦。我们需要求公共弦 $OD$ 的长度。我们知道，弦的垂直平分线经过圆心。所以，$OC = CD$ 且 $\angle ACO =\angle BCO = 90^o$。在 $\triangle ACO$ 中，$AO^2 = AC^2+CO^2$$5^2 ... 阅读更多
**已知：**圆的两条相等弦在圆内相交。
**已知：**圆的两条相等弦在圆内相交。