数据结构
网络
关系数据库管理系统 (RDBMS)
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C语言编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理学
化学
生物学
数学
英语
经济学
心理学
社会学
服装学
法学
已知：球体的表面积为 $154\ cm^{2}$。求解：求球体的半径。解：设球体的半径为 $r$。则球体的表面积 $=4\pi r^2 = 154$，所以 $r^2=\frac{154}{4\pi} = \frac{154}{4\times\frac{22}{7}} = \frac{154\times7}{4\times22} = \frac{49}{4} = \frac{7^2}{2^2}$，$r=\frac{7}{2} = 3.5\ cm$。因此，球体的半径为 $3.5\ cm$。
已知：一个半球形碗是用厚度为 $0.25\ cm$ 的钢材制成的。碗的内半径为 $5\ cm$。求解：求制作碗所用钢材的体积。解：钢材厚度 $= 0.25\ cm = \frac{1}{4}\ cm$，碗的内半径 $(r) = 5\ cm$，则外半径 $(R) = 5 + 0.25 = 5.25\ cm$。所以，所用钢材的体积 $= \frac{2}{3} \pi(R^3-r^3) = \frac{2}{3} \times \frac{22}{7} \times[(5.25)^{3}-(5.00)^{3}] = \frac{44}{21}(144.703125-125.000000) = \frac{44}{21} \times 19.703125 = 41.28 \mathrm{~cm}^{3}$。碗的外曲面面积为 $41.28 \mathrm{~cm}^{3}$。
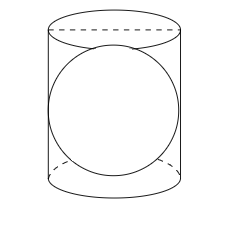
"\已知：一个正圆柱体刚好包围一个半径为 \( r \) 的球体。求解：(i) 球体的表面积，(ii) 圆柱体的侧面积，(iii) (i) 和 (ii) 中所得面积的比率。解：(i) 半径为 $r$ 的球体的表面积 $= 4\pi r^2$ (ii) 圆柱体的高度 $h =$ 球体的直径 $= r + r = 2r$，圆柱体的高度为 $2r$。圆柱体的半径 $= r$，圆柱体的侧面积 $= 2\pi rh = 2\pi r(2r) = 4\pi r^2$ (iii) 球体的表面积与圆柱体侧面积的比率为…… 阅读更多
已知：圆锥体的底面直径为 \( 10.5 \mathrm{~cm} \)，斜高为 \( 10 \mathrm{~cm} \)。求解：求其侧面积。解：圆锥体底面直径 $=10.5\ cm$，半径$=\frac{直径}{2}=\frac{10.5}{2}=5.25\ cm$，斜高 $=10\ cm$，则侧面积 $=\pi r l = \frac{22}{7} \times 5.25 \times 10 = \frac{22}{7}\times52.5 = 165 \mathrm{~cm}^{2}$。因此，圆锥体的侧面积为 $165 \mathrm{~cm}^{2}$。
已知：圆锥体的斜高为 $21\ m$，底面直径为 $24\ m$。求解：求圆锥体的表面积。解：斜高 $(l) = 21\ m$，底面直径 $= 24\ m$，半径 $(r) = \frac{24}{2} = 12\ m$。则表面积 $= \pi r(l + r) = \frac{22}{7} \times 12(21+12) = \frac{22}{7} \times 12 \times 33 = \frac{8712}{7} = 1244.57 \mathrm{~m}^{2}$。因此，圆锥体的表面积为 $1244.57 \mathrm{~m}^{2}$。
已知：圆锥体的侧面积为 $308\ cm^2$，斜高为 $14\ cm$。求解：求底面半径和圆锥体的表面积。解：侧面积 $= 308\ cm^2$，斜高 $(l) = 14\ cm$，则底面半径 $(r) = \frac{侧面积}{πl} = \frac{308 \times 7}{22 \times 14} = 7\ cm$。表面积 $=\pi r l + \pi r^2 = 308 + \frac{22}{7} \times 7 \times 7 = 308 + 154 = 462\ cm^2$。因此，底面半径和表面积分别为…… 阅读更多
已知：一个圆锥形帐篷高 $10\ m$，底面半径为 $24\ m$。每 $1\ m^2$ 帆布成本为 $Rs.\ 70$。求解：求帐篷的斜高和制作帐篷所需的帆布成本。解：圆锥形帐篷高度 $h= 10\ m$，底面半径 $(r) = 24\ m$，斜高 $(l) = \sqrt{r^2 + h^2} = \sqrt{24^2 + 10^2} = \sqrt{676} = 26\ m$。侧面积 $=\pi r l = \frac{22}{7} \times 24 \times 26$，每 $1\ m^2$ 帆布成本为 $Rs.\ 70$，则总成本 $= Rs.\ \frac{22}{7} \times 24 \times 26 \times ... 阅读更多
已知：圆锥形帐篷高度为 $8\ m$，底面半径为 $6\ m$。篷布宽度为 $3\ m$。求解：求所需的篷布长度。解：圆锥形帐篷高度 $(h) = 8\ m$，底面半径 $(r) = 6\ m$，斜高 $(l) = \sqrt{r^2 + h^2} = \sqrt{6^2 + 8^2} = \sqrt{100} = 10\ m$。侧面积 $= \pi rl = 3.14 \times 6 \times 10 = 188.4\ m^2$。篷布宽度 $= 3\ m$，则所需的篷布长度 $= \frac{188.4}{3} = 62.8\ m$。所需额外长度 $= 20\ cm = 0.2\ m$，总长度为…… 阅读更多
已知：一个圆锥形坟墓的斜高和底面直径分别为 $25\ m$ 和 $14\ m$。求解：求以每 $100\ m^2$ 210卢比的价格粉刷其曲面的成本。解：斜高 $(l) = 25\ m$，底面直径 $= 14\ m$，半径 $(r) = \frac{14}{2} = 7\ m$。侧面积 $=\pi r l = \frac{22}{7} \times 7 \times 25 = 550\ m^2$。粉刷价格为每 $100\ m^2$ 210卢比，则总成本 $= \frac{550 \times 210}{100} = 1155$ 卢比。粉刷曲面的总成本为…… 阅读更多
已知：一个小丑帽的形状是底面半径为 7 厘米，高为 24 厘米的直圆锥体。