已知:框架的底部直径为 \( 20 \mathrm{~cm} \),高度为 \( 30 \mathrm{~cm} \)。需要留出 \( 2.5 \mathrm{~cm} \) 的余量用于折叠到框架的顶部和底部。求解:我们需要计算覆盖灯罩所需的布料面积。解:底部的直径 $d=20\ cm$底部的半径 $r =\frac{20}{2}$$=10\ cm$灯罩的高度 $h = 30\ cm$留出 $2.5\ cm$ 的余量用于折叠到顶部和底部。这意味着,框架的总高度 $H = 30 + 2.5 + 2.5$$H = ... 阅读更多
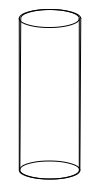
已知:每个笔筒的半径为 $3\ cm$,高度为 $10.5\ cm$。共有 $35$ 名参赛者。求解:我们需要计算比赛所需的硬纸板面积。解:圆柱形笔筒的半径 $(r) = 3\ cm$笔筒的高度 $(h) = 10.5\ cm$因此,笔筒的表面积 $=2 \pi r h+\pi r^{2}$$=\pi r(2 h+r)$$=\frac{22}{7} \times 3(2 \times 10.5+3)$$=\frac{66}{7}(21+3)$$=\frac{66}{7} \times 24$$=\frac{1584}{7} \mathrm{~cm}^{2}$制作的笔筒数量 $=35$这意味着,所需硬纸板的总面积 $=\frac{1584}{7} \times 35$$=7920 \mathrm{~cm}^{2}$因此,所需硬纸板的总面积为 $7920 \mathrm{~cm}^{2}$。阅读更多
已知:\( \mathrm{ABC} \) 和 \( \mathrm{BDE} \) 是两个等边三角形,\( \mathrm{D} \) 是 \( \mathrm{BC} \) 的中点。\( \mathrm{AE} \) 与 \( \mathrm{BC} \) 相交。求证:(i) \( \operatorname{ar}(\mathrm{BDE})=\frac{1}{4} \operatorname{ar}(\mathrm{ABC}) \)(ii) \( \operatorname{ar}(\mathrm{BDE})=\frac{1}{2} \operatorname{ar}(\mathrm{BAE}) \)(iii) \( \operatorname{ar}(\mathrm{ABC})=2 \) ar \( (\mathrm{BEC}) \)(iv) \( \operatorname{ar}(\mathrm{BFE})=\operatorname{ar}(\mathrm{AFD}) \)(v) \( \operatorname{ar}(\mathrm{BFE})=2 \operatorname{ar}(\mathrm{FED}) \)(vi) \( \operatorname{ar}(\mathrm{FED})=\frac{1}{8} \operatorname{ar}(\mathrm{AFC}) \)证明:连接 \( \mathrm{EC} \) 和 \( \mathrm{AD} \)设 $G$ 和 $H$ 分别是边 $AB$ 和 $AC$ 的中点。连接 $G$ 和 $H$。$GH$ 平行于 $BC$。根据中点定理,$GH=\frac{1}{2}BC$$GH=BD=DC$类似地,$GD = AH = CH$$DH = AG = BG$这... 阅读更多
已知:四边形 \( \mathrm{ABCD} \) 的对角线 \( \mathrm{AC} \) 和 \( \mathrm{BD} \) 相交于 \( \mathrm{P} \)。求证:ar \( (\mathrm{APB}) \times \operatorname{ar}(\mathrm{CPD})=\operatorname{ar}(\mathrm{APD}) \times \operatorname{ar}(\mathrm{BPC}) \)。证明:作 $AM$ 垂直于 $BD$,$CN$ 垂直于 $BD$$ar(\triangle ABP) = \frac{1}{2}\times BP \times AM$…………..(i)$ar(\triangle APD) = \frac{1}{2}\times DP \times AM$…………..(ii)将 (ii) 除以 (i),得到, $\frac{\operatorname{ar}(\triangle \mathrm{APD})}{\operatorname{ar}(\triangle \mathrm{ABP})}=\frac{\frac{1}{2} \times \mathrm{DP} \times \mathrm{AM}}{\frac{1}{2} \times \mathrm{BP} \times \mathrm{AM}}$$\frac{ar(APD)}{ar(ABP)}= \frac{DP}{BP}$…….....(iii)类似地, $\frac{ar(CDP)}{ar(BPC)} = \frac{DP}{BP}$……. (iv)从 (iii) 和 (iv) 可以得到, $\frac{ar(APD)}{ar(ABP)} = \frac{ar(CDP)}{ar(BPC)}$ $ar(APD) \times ar(BPC) = ar(ABP) \times ar (CDP)$证毕。阅读更多
PQ是中线……阅读更多
该圆柱体底部的直径为2m。
因此,总表面积为7.48 m²。
(ii) 外侧曲面……阅读更多
证毕。阅读更多

 数据结构
数据结构 网络
网络 关系数据库管理系统 (RDBMS)
关系数据库管理系统 (RDBMS) 操作系统
操作系统 Java
Java iOS
iOS HTML
HTML CSS
CSS Android
Android Python
Python C 编程
C 编程 C++
C++ C#
C# MongoDB
MongoDB MySQL
MySQL Javascript
Javascript PHP
PHP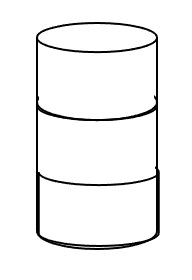 "\
"\


 "\
"\ "\
"\