已知:给出了用彩色纸制作的飞机的图形。求解:我们必须找到所用彩色纸的总面积。解答:所用纸张的总面积 = 部分 I + 部分 II + 部分 III + 部分 IV + 部分 V部分 I:这是一个等腰三角形,边长为 $a = 1\ cm, b = 5\ cm, c = 5\ cm$。半周长,$S = \frac{a+ b + c}{2}$$S = \frac{1+ 5 + 5}{2}$ $S= \frac{11}{2}$$S = 5.5\ cm$三角形的面积 $= \sqrt {S (S-a)(S-b)(S-c)}$$= \sqrt {5.5 (5.5-1)(5.5-5)(5.5-5)}$$= \sqrt {5.5 (4.5)(0.5)(0.5)}$$= 0.75 \sqrt{11}\ cm^2$部分 I $= ... 阅读更多
已知:四边形 $ABCD$ 的 $AB=3\ cm$,$BC=4\ cm$,$CD=4\ cm$,$DA=5\ cm$ 和 $AC=5\ cm$。要求:我们必须找到四边形 $ABCD$ 的面积。解答: 在 $\triangle ABC$ 中,使用勾股定理,$AC^2=AB^2+BC^2$$5^2=3^2+4^2$$25=25$因此,$\triangle ABC$ 的面积 = $\frac{1}{2}\times3\times4=6\ cm^2$在 $\triangle ACD$ 中,$s=\frac{1}{2}(5+5+4)$$=\frac{14}{2}$$=7\ cm$$\triangle ACD$ 的面积 = $\sqrt{s(s-a)(s-b)(s-c)}$$=\sqrt{7(7-5)(7-5)(7-4)}$$=\sqrt{(7)(2)(2)(3)}$$=2\sqrt{21}\ cm^2$$=9.17\ cm^2$因此,四边形 $ABCD$ 的面积 = $\triangle ABC$ 的面积 + $\triangle ACD$ 的面积因此,四边形 $ABCD$ 的面积 = $6\ cm^2+9.17\ cm^2$$=15.17\ cm^2$。四边形 $ABCD$ 的面积为 $15.17\ cm^2$。 阅读更多
已知:$BC=8\ cm, \angle B=45^o$ 和 $AB-AC=3.5\ cm$。要求:我们必须构造一个 $\triangle ABC$。作图步骤:(i) 我们画一条长度为 $8\ cm$ 的线段 $BC$。(ii) 现在,构造一个角 $XBC$,使得 $\angle XBC=45^o$(iii) 现在,用圆规测量 $AB-AC=3.5\ cm$,从点 $B$ 画一条弧,并在射线 $BX$ 上标记为点 $D$。(iv) 现在,让我们连接 $DC$。然后用圆规画出 $DC$ 的垂直平分线,并将平分线与射线 $BX$ 的交点标记为点 $A$。(v) 现在,... 阅读更多
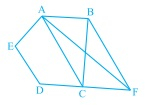
已知:$ABCDE$ 是一个五边形。过 \( \mathrm{B} \) 的一条平行于 \( \mathrm{AC} \) 的线与 \( \mathrm{DC} \) 的延长线交于 $F$。要求:我们必须证明(i) \( \operatorname{ar}(\mathrm{ACB})=\operatorname{ar}(\mathrm{ACF}) \)(ii) \( \operatorname{ar}(\mathrm{AEDF})=\operatorname{ar}(\mathrm{ABCDE}) \)解答:$ABCDE$ 是一个五边形,$BF \| AC$。(i) $\triangle ACB$ 和 $\triangle ACF$ 在同一条底 $AC$ 上,并且在平行线 $AC$ 和 $BF$ 之间。因此,$ar (\triangle ACB) = ar (\triangle ACF)$........…(i)(ii) $ar (AEDF) = ar (AEDC + ar (\triangle ACF)$$=ar (AEDC) + ar (\triangle ACB)$ [来自 (i)]$= ar (ABCDE)$证毕。
已知:梯形 \( \mathrm{ABCD} \) 的对角线 \( \mathrm{AC} \) 和 \( \mathrm{BD} \) 与 \( \mathrm{AB} \| \mathrm{DC} \) 交于 \( \mathrm{O} \)。要求:我们必须证明 ar \( (\mathrm{AOD})=\operatorname{ar}(\mathrm{BOC}) \)。解答:$\triangle ABC$ 和 $\triangle ABD$ 在同一条底 $AB$ 上,并且在平行线 $AB$ 和 $CD$ 之间。这意味着,$ar (\triangle ABD) = ar (\triangle ABC)$从两边减去 $ar (\triangle AOB)$,得到,$ar (\triangle ABD) - ar (\triangle AOB) = ar (\triangle ABC) - ar (\triangle AOB)$$ar (\triangle AOD) = ar (\triangle BOC)$证毕。
已知:\( \mathrm{XY} \) 是三角形 \( \mathrm{ABC} \) 的边 \( \mathrm{BC} \) 的平行线。\( \mathrm{BE} \| \mathrm{AC} \) 和 \( \mathrm{CF} \| \mathrm{AB} \) 分别与 \( \mathrm{XY} \) 交于 \( \mathrm{E} \) 和 \( F \)。要求:我们必须证明 \( \operatorname{ar}(\mathrm{ABE})=\operatorname{ar}(\mathrm{ACF}) \)。解答:$BE \| AC$这意味着,$BE \| CY$$CF \| AB$这意味着,$CF \| XB$$XY \| BC$ 和 $CY \| BE$因此,$EYCB$ 是一个平行四边形。$\triangle \mathrm{ABE}$ 和平行四边形 $EYCB$ 在同一条底 $BE$ 上,并且在平行线 $B E$ 和 $A C$ 之间。这意味着,$ar(\triangle \mathrm{ABE})=\frac{1}{2} ar(\mathrm{EYCB})$........(i)$C F \| A B$ 和 ... 阅读更多
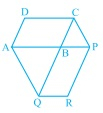
**已知:**平行四边形ABCD的边AB延长到任意一点P。过A且平行于CP的直线交CB的延长线于Q,然后补全平行四边形PBQR。**求证:**ar(ABCD) = ar(PBQR)。**证明:**连接AC和PQ。PQ和AC分别是平行四边形PBQR和ABCD的对角线。因此,我们知道,平行四边形的一条对角线将其分成两个面积相等的三角形。这意味着,ar(△ABC) = 1/2 ar(ABCD) ......(i)ar(△PBQ) = 1/2 ar(PBQR) ......(ii)△ACQ和△AQP同底AQ且... 阅读更多
**已知:**在△ABC中,D和E分别是AB和AC上的点,使得ar(DBC) = ar(EBC)。**求证:**DE∥BC。**证明:**ar(DBC) = ar(EBC)这意味着,△DBC和△EBC面积相等且有相同的底BC。因此,△DBC和△EBC位于相同的平行线之间。这意味着,DE∥BC证毕。
**已知:**墙的边长为15m、11m和6m。**求解:**我们需要找到用颜色涂抹的墙的面积。**解:**墙的边长为15m、11m和6m。根据海伦公式:A = √[s(s-a)(s-b)(s-c)]因为,S = (a+b+c)/2S = (15m + 11m + 6m)/2S = 32m/2S = 16m这意味着,A = √[16(16-15)(16-11)(16-6)]A = √[16(1)(5)(10)]A = √800 m²A = 20√2 m²因此,用颜色涂抹的墙的面积为20√2 m²。
**已知:**三角形的两条边长分别为18cm和10cm,周长为42cm。**求解:**我们需要找到三角形的面积。**解:**假设三角形的第三条边长为x这意味着,三角形的三条边长分别为18cm、10cm和xcm。我们有,三角形的周长为42cm我们知道,周长P是一个边长分别为a单位、b单位和c单位的三角形的周长P=(a+b+c)单位。这意味着,42cm = 18cm + 10cm + xcm42cm = 28cm + xcm这意味着,xcm = 42cm - 28cmxcm = 14cm根据海伦公式:A = √[s(s-a)(s-b)(s-c)]因为,S = (a+b+c)/2S = (18+10+12)/2S = 42/2S = 21cm这意味着,A = √[21(21-18)(21-10)(21-14)]A = √[21(3)(11)(7)]A = 21√11... 阅读更多

 数据结构
数据结构 网络
网络 关系数据库管理系统
关系数据库管理系统 操作系统
操作系统 Java
Java iOS
iOS HTML
HTML CSS
CSS Android
Android Python
Python C 编程
C 编程 C++
C++ C#
C# MongoDB
MongoDB MySQL
MySQL Javascript
Javascript PHP
PHP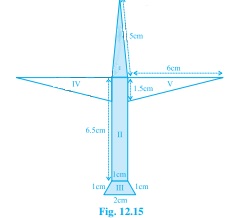 "\
"\
 "\
"\ "\
"\