数据结构
网络
关系数据库管理系统 (RDBMS)
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 语言编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理学
化学
生物学
数学
英语
经济学
心理学
社会学
服装学
法学
已知：一个边长为 7cm 的立方体上放置一个半球体。求解：我们需要找到半球体可以具有的最大直径以及这个立体的表面积。解答：立方体的边长，a = 7 cm立方体最长对角线 = a√2 cm = 7√2 cm由于立方体上放置一个半球体，因此立方体的边长应该等于半球体的直径。球体的直径 = 7 cm球体的半径，r = 7/2 cm立体的总表面积 = 立方体的总表面积 - 半球体的内部截面面积… 阅读更多
已知：从一个立方体木块的一个面上挖出一个半球形的凹槽，使得半球体的直径 l 等于立方体的边长。求解：我们需要求出剩余立体的表面积。解答：立方体木块的边长 a = l这意味着，挖出的半球体的直径 = l半球体的半径 r = l/2因此，立方体的体积 = a³ = l³ 立方单位半球体的体积 = (2/3)πr³ = (2/3) × π × (l/2)³ = (1/12)πl³ 立方单位剩余木块的总表面积 = 6a² + 2πr² - πr² = 6a² + πr² = 6 × l² + π… 阅读更多
"
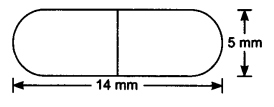
已知：一个药丸的形状是一个圆柱体，两端各粘着一个半球体（见图）。整个药丸的长度是 14 毫米，药丸的直径是 5 毫米。求解：我们需要求出它的表面积。解答：每个半球形末端的直径 = 5 毫米这意味着，每个半球形末端的半径 = 5/2 毫米因此，每个半球形末端的表面积 = 2πr² = 2 × (22/7) × (5/2) × (5/2) = 275/7 mm²两个半球形末端的表面积总和 = (2 × 275)/7 mm² = 550/7 mm²药丸的总长度 = 14 毫米圆柱表面的长度 = 总长度 - 半径… 阅读更多
"
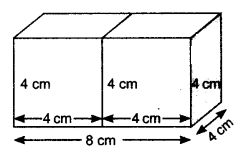
已知：两个体积均为 64 cm³ 的立方体端对端连接。求解：我们需要求出所得长方体的表面积。解答：每个立方体的体积 = 64 cm³这意味着，立方体的边长 = ³√64 = 4 cm将两个立方体连接后形成的长方体的长度 (l) = 4 + 4 = 8 cm长方体的宽度 (b) = 4 cm长方体的高度 (h) = 4 cm因此，所得长方体的表面积 = 2(lb + bh + lh) = 2(8 × 4 + 4 × 4 + 4 × 8) = 2(32 + 16 + 32) = 2 × 80 = 160 cm²。
"
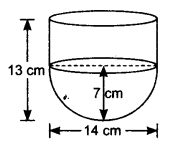
已知：一个容器由一个空心半球体和一个空心圆柱体组成。半球体的直径为 14 厘米，容器的总高度为 13 厘米。求解：我们需要求出容器的内表面积。解答：半球体的直径 = 14 cm这意味着，半球体的半径 = 14/2 = 7 cm半球体的曲面面积 = 2πr² = 2 × (22/7) × 7 × 7 = 308 cm²圆柱部分的半径 = 半球体的半径 = 7 cm圆柱体的高度 = 总高度 - 半球体的半径 = 13 - 7 = 6 cm圆柱体的曲面面积 = 2πrh = 2… 阅读更多
"
已知：正方形的边长 = 8 cm象限的半径 = 8 cm求解：我们需要计算图中所示区域的面积。解答：正方形的边长 = 8 cm正方形的面积 = 8² = 64 cm²象限的半径 = 8 cm象限的面积 = (πr²θ)/360° = (22/7) × (8 × 8 × 90°)/360° = (22 × 2 × 8)/7 = 352/7正方形面积减去一个象限的面积 = 正方形的面积 - 象限的面积 = 64 - 352/7 = (448 - 352)/7 = 96/7 cm²阴影区域的面积 = 正方形的面积 - 2 × (正方形面积减去一个象限的面积)… 阅读更多
"
已知：ABC是半径为14厘米的四分之一圆，以BC为直径作半圆。 求：求阴影部分的面积。 解： 圆的四分之一圆的半径 = 14 厘米 三角形ABC是直角三角形 AB=AC=14厘米 BC²=AB²+AC² =(14)²+(14)² BC=√(2×14) =14√2 厘米 因此，半圆BDC的半径r =BC/2 =14√2/2厘米 =7√2厘米 阴影部分面积 = 半圆面积 - 四分之一圆ABC面积 - 三角形ABC面积 =πr²/2-[90°/360°×π(14)²-1/2×AC×AB] =π[(7√2)²/2]-[(π(14)²)/4-1/2×14×14] =[(22×7×7×2)/(7×2)]-[(22×14… 阅读更多
"
方框中三种金属和三种非金属的名称如下： 金属：铁、铜、铝 非金属：碳、氧、硫
"
已知：AB和CD分别是半径分别为21厘米和7厘米的两个同心圆的弧，圆心为O。∠AOB=30°。 求：求阴影部分的面积。 解： 扇形AOB的半径 = 21厘米 因此，扇形AOB的面积 = πr²θ/360° = (22/7) × (21 × 21 × 30°)/360° = (11 × 21)/2 = 231/2 厘米² 扇形COD的半径 = 7厘米 ∠COD = 30° 因此，扇形COD的面积 = πr²θ/360° = (22/7) × (7 × 7 × 30°)/360° = 77/6 厘米² 阴影部分面积 = 扇形AOB面积 - 扇形COD面积 = 231/2 - 77/6 = (693-77)/6 = 616/6 = 308/3 厘米² 阴影部分的面积是308/3厘米²。阅读更多