数据结构
网络
关系数据库管理系统
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理学
化学
生物学
数学
英语
经济学
心理学
社会学
服装设计
法律研究
已知：一位弓箭手在瞄准目标时拉弓。然后她松开弓弦，箭开始向目标飞去。需要做：填写空白处。解答：在填写空白处之前，让我们简单讨论一下给定情况：当弓箭手拉弓时，她施加了肌肉力，拉伸后的弓的形状发生了变化，当弓箭手松开弓弦时，箭开始向目标飞去。箭从静止状态开始运动。因此，接触力是箭在... 阅读更多
"
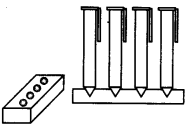
已知：一个木制的笔筒呈长方体形状，有四个圆锥形的凹槽用来放笔。长方体的尺寸为 15 厘米×10 厘米×3.5 厘米。每个凹槽的半径为 0.5 厘米，深度为 1.4 厘米。需要做：我们需要求整个笔筒的木材体积。解答：长方体笔筒的长度 $l = 15\ cm$长方体笔筒的宽度 $b = 10\ cm$长方体笔筒的高度 $h = 3.5\ cm$因此，长方体笔筒的体积 $= lbh$$= 15 \times ... 阅读更多
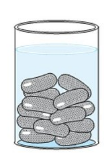
一个容器呈倒置圆锥形。它的高度为 8 厘米，开口顶部的半径为 5 厘米。它装满水直至边缘。当将一些铅弹（每个铅弹都是半径为 0.5 厘米的球体）放入容器中时，四分之一的水流出。求放入容器中的铅弹数量。
已知：一个容器呈倒置圆锥形。它的高度为 8 厘米，开口顶部的半径为 5 厘米。它装满水直至边缘。当将一些铅弹（每个铅弹都是半径为 0.5 厘米的球体）放入容器中时，四分之一的水流出。需要做：我们需要求放入容器中的铅弹数量。解答：圆锥的高度 $=8 \mathrm{~cm}$圆锥的半径 $=5 \mathrm{~cm}$这意味着，圆锥的体积 $=\frac{1}{3} \pi r^{2} h$$=\frac{1}{3} \pi(5)^{2} \times 8$$=\frac{200}{3} \pi \mathrm{cm}^{3}$铅弹的半径 ... 阅读更多
已知：一根实心的铁杆由一个高 220 厘米、底直径 24 厘米的圆柱体和一个高 60 厘米、半径 8 厘米的圆柱体叠加而成。需要做：我们需要求这根铁杆的质量，已知 $1\ cm^3$ 铁的质量约为 8 克。解答：第一个圆柱体的半径 $= 12\ cm$第一个圆柱体的高度 $= 220\ cm$因此，第一个圆柱体的体积 $= \pi r^2h$$= \pi (12)^2 (220)$$= 144 \times 220 \pi$$= 144 \times 220 \times 3.14$$= 99475.2\ cm^3$.......(i)第二个 ... 阅读更多
已知：一个固体由一个圆锥体和一个半球体叠加而成，它们的半径均为 1 厘米，圆锥体的高度等于其半径。需要做：我们需要求这个固体的体积（用 $\pi$ 表示）。解答：半球的半径 $=1 \mathrm{~cm}$圆锥部分的高度 $=1 \mathrm{~cm}$这意味着，固体的总高度 $=1+1=2 \mathrm{~cm}$因此，固体的体积 $=$ 圆锥部分的体积 $+$ 半球部分的体积$=\frac{1}{3} \pi r^{2} h+\frac{2}{3} \pi r^{3}$$=\frac{1}{3} \pi r^{2}(h+2 r)$$=\frac{1}{3} \pi \times(1)^{2}[1+2 \times1]$$=\frac{\pi}{3} \times 1 \times 3$$=\pi \mathrm{~cm}^{3}$固体的体积 ... 阅读更多
已知：瑞秋，一名工程专业的学生，被要求用薄铝片制作一个模型，模型的形状是一个圆柱体，两端各连接一个圆锥体。模型的直径为 3 厘米，长度为 12 厘米。每个圆锥体的高度为 2 厘米。需要做：我们需要求瑞秋模型中包含的空气体积。解答：模型中包含的空气体积 $=$ 固体的总体积每个圆锥体底部的直径 $= 3\ cm$这意味着，每个圆锥体底部的半径 $= \frac{3}{2}\ cm$每个圆锥体的高度 $= 2\ cm$体积 ... 阅读更多
"
已知：一个古拉布·贾蒙（Gulab Jamun）含有糖浆，糖浆的体积约占其总体积的30%。要求：我们要求出大约有多少糖浆存在于45个古拉布·贾蒙中，每个古拉布·贾蒙的形状像一个圆柱体，两端是半球形，长度为5厘米，直径为2.8厘米。解答：一个古拉布·贾蒙的体积=圆柱部分的体积+两个半球形末端的体积每个半球形部分的半径$= \frac{2.8}{2}$$= 1.4\ cm$一个半球形末端的体积 $=\frac{2}{3} \pi r^{3}$$=\frac{2}{3} \times \frac{22}{7}(1.4)^{3}$$=\frac{2}{3} \times \frac{22}{7} \times (1.4)^3$$=\frac{2 \times 22 \times 2 \times 14 \times 14}{3 \times 10 \times 10 \times ... 阅读更多
已知：从一个高为\( 2.4 \mathrm{~cm} \)和直径为\( 1.4 \mathrm{~cm} \)的实心圆柱体中，挖出一个相同高度和相同直径的圆锥形空腔。要求：我们要求出剩余实心体的总表面积。解答：实心圆柱体的直径$= 1.4\ cm$这意味着，圆柱体的半径 $r = \frac{1.4}{2}$$ = 0.7\ cm$圆柱体的高度 $h = 2.4\ cm$圆锥体的半径 $r = 0.7\ cm$圆锥体的高度 $h = 2.4\ cm$圆锥体的斜高 $l=\sqrt{r^{2}+h^{2}}$$=\sqrt{(0.7)^{2}+(2.4)^{2}}$$=\sqrt{0.49+5.76}$$=\sqrt{6.25}$$=2.5 \mathrm{~cm}$剩余实心体的总表面积=圆柱体的表面积+圆柱体底面的表面积... 阅读更多
"
已知：圆柱体的高度，$h=10\ cm$，底部的半径，$r=3.5\ cm$。要求：我们要求出该物品的总表面积。解答：设 $r$ 为圆柱体底部的半径，$h$ 为其高度。这意味着，物品的总表面积=圆柱体的侧面积+2个（半球体的表面积）$=2\pi rh+2( 2 \pi r^{2})$$=2\pi r( h+2r)$$=2\times \frac{22}{7}\times3.5( 10+2\times3.5)$$=374\ cm^{2}$ 因此，该物品的总表面积为 $374\ cm^{2}$。
已知：一个帐篷的形状是一个圆柱体上面加一个圆锥形的顶部。圆柱体部分的高度和直径分别为$2.1\ m$和$4\ m$，顶部的斜高为$2.8\ m$。要求：我们要求出制作帐篷所需的帆布的成本，帆布的价格为每平方米500卢比。解答：对于圆锥部分，我们有$r=2\ m$和$l=2.8\ m$$\therefore \ S_{1}=$圆锥部分的侧面积$\therefore \ S_{1} \ =\ \pi rl$$=\pi \times \ 2\ \times \ 2.8$$=\ 5.6\pi \ m^{2}$对于圆柱部分，我们有$r =2\ ... 阅读更多