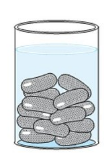
一个古拉布·贾蒙（Gulab Jamun）含糖浆的体积约占其总体积的30%。假设每个古拉布·贾蒙的形状都是一个长5厘米、直径2.8厘米的圆柱体，两端各有一个半球形（见图），试求45个古拉布·贾蒙大约含有多少糖浆。
"

已知

一个古拉布·贾蒙（Gulab Jamun）含糖浆的体积约占其总体积的30%。

要求

我们必须求出45个古拉布·贾蒙大约含有多少糖浆，每个古拉布·贾蒙的形状都是一个长5厘米、直径2.8厘米的圆柱体，两端各有一个半球形。

解答

一个古拉布·贾蒙的体积

$=$ 圆柱部分的体积 $+$ 两个半球形部分的体积

每个半球形部分的半径 $= \frac{2.8}{2}$

$= 1.4\ cm$

一个半球形部分的体积 $=\frac{2}{3} \pi r^{3}$

$=\frac{2}{3} \times \frac{22}{7}(1.4)^{3}$

$=\frac{2}{3} \times \frac{22}{7} \times (1.4)^3$

$=\frac{2 \times 22 \times 2 \times 14 \times 14}{3 \times 10 \times 10 \times 10}$

$=5.74 \mathrm{~cm}^{3}$

两个半球形部分的体积 $= 2 \times 5.74$

$= 11.48\ cm^3$

圆柱部分的高度 $=$ 总高度 $-$ 两个半球形部分的半径

$= 5-2(1.4)\ cm$

$= 5-2.8$

$= 2.2\ cm$

圆柱部分的半径 $= 1.4\ cm$

古拉布·贾蒙圆柱部分的体积 $= \pi r^2h$

$= \frac{22}{7} \times (1.4)^2 \times 2.2$

$= 22\times2\times1.4\times2.2$

$= 13.55\ cm^3$

一个古拉布·贾蒙的总体积 $=$ 两个半球形部分的体积 $+$ 圆柱部分的体积

$= 11.48+ 13.55$

$= 25.03\ cm^3$

糖浆的体积 $= 30 \%$ 的古拉布·贾蒙的体积

$= \frac{30}{100} \times 25.03$

$= 7.50\ cm^3$

因此，

45个古拉布·贾蒙中糖浆的体积

$= 45 \times$ （一个古拉布·贾蒙中糖浆的体积）

$= 45 \times 7.50$

$= 337.5\ cm^3$

$= 338\ cm^3$

教程点

更新于: 2022年10月10日

53 次查看

开启你的职业生涯

通过完成课程获得认证

开始学习